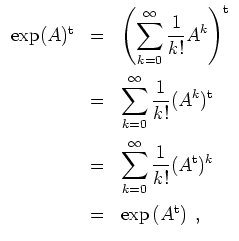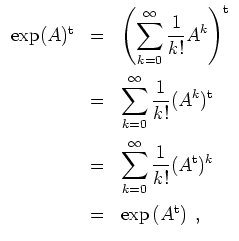Lösung.

1.
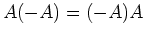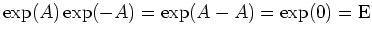Da $ \mbox{$A(-A) = (-A)A$}$ , ist $ \mbox{$\exp(A)\exp(-A) = \exp(A - A) = \exp(0) = \text{E}$}$ .
2.
Nach Definition ist
$ \mbox{$\displaystyle \begin{array}{rcl} \exp(A)^\text{t} & = & \left(\displa... ...})^k \vspace*{2mm}\\ & = & \exp\left(A^\text{t}\right)\; , \\ \end{array}$}$
wobei die erste Gleichheit gilt, da die Reihe eintragsweise konvergiert.
3.
Es ist
$ \mbox{$\displaystyle \exp((s+t)A) \;=\; \exp(sA+tA) \;=\; \exp(sA)\exp(tA)\; , $}$
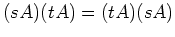da $ \mbox{$(sA)(tA) = (tA)(sA)$}$ .
4.
Es ist
$ \mbox{$\displaystyle \exp(\lambda\text{E} + A) \;=\; \exp(\lambda\text{E})\exp(A) \;=\; \exp(\lambda)\exp(A) \; , $}$
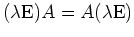da $ \mbox{$(\lambda \text{E}) A = A (\lambda \text{E})$}$ .
5.
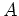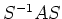Da beide Seiten invariant unter Konjugation sind, d.h. unter Übergang von $ \mbox{$A$}$ nach $ \mbox{$S^{-1}A S$}$ für eine invertierbare Matrix 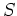$ \mbox{$S$}$ , dürfen wir 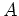$ \mbox{$A$}$ als in Jordanform gegeben annehmen. Da beide Seiten, auf eine Blockhauptdiagonalmatrix angewandt, sich multiplikativ in die Blöcke zerlegen, dürfen wir annehmen, daß 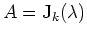$ \mbox{$A = \text{J}_k(\lambda)$}$ für ein 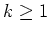$ \mbox{$k\ge 1$}$ und ein 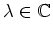$ \mbox{$\lambda\in\mathbb{C}$}$ . Nun folgt
$ \mbox{$\displaystyle \det(\exp(\text{J}_k(\lambda))) \;=\; \exp(\lambda)^k \;=\; \exp(k\lambda) \;=\; \exp(\text{Spur }\text{J}_k(\lambda))\; . $}$