Lösung.

Es ist
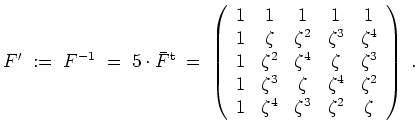
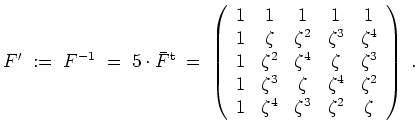
$ \mbox{$\displaystyle F' \; := \; F^{-1} \; = \; 5\cdot \bar{F}^\text{t} \; = ... ...a^2 \\ 1 & \zeta^4 & \zeta^3 & \zeta^2 & \zeta \\ \end{array}\right)\;. $}$
Zum Eigenwert $ \mbox{$-5^{1/2}$}$ hat $ \mbox{$F'$}$ einen Eigenvektor
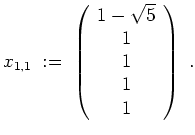
$ \mbox{$\displaystyle x_{1,1} \;:=\; \left( \begin{array}{c} 1 - \sqrt{5} \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array}\right)\;. $}$
Zum Eigenwert $ \mbox{$5^{1/2}$}$ hat $ \mbox{$F'$}$ Eigenvektoren
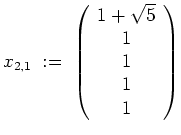
$ \mbox{$\displaystyle x_{2,1} \;:=\; \left( \begin{array}{c} 1 + \sqrt{5} \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array}\right) $}$
und
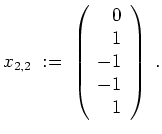
$ \mbox{$\displaystyle x_{2,2} \;:=\; \left( \begin{array}{r} 0 \\ 1 \\ -1 \\ -1 \\ 1 \\ \end{array}\right)\;. $}$
Sei $ \mbox{$V := \langle x_{1,1},\, x_{2,1},\, x_{2,2} \rangle$}$ . Es ist $ \mbox{$F'v\in V$}$ für alle $ \mbox{$v\in V$}$ .

Wir behaupten, daß $ \mbox{$F'w\in V^\perp$}$ für alle $ \mbox{$w\in V^\perp = \left\{ x\in\mathbb{C}^n\; \vert\; \bar{v}^{\text{t}} x = 0 \text{ f\uml ur alle }v\in V\right\}$}$ .

Da $ \mbox{$F'$}$ normal, und somit unitär diagonalisierbar ist, finden wir (auf theoretischem Wege) eine unitäre Matrix $ \mbox{$U$}$ und eine Diagonalmatrix $ \mbox{$D$}$ mit $ \mbox{$F' = \bar{U}^\text{t} D U$}$ , i.e. $ \mbox{$D = U F' \bar{U}^\text{t}$}$ . Genauer, wir können $ \mbox{$U$}$ so wählen, daß die ersten drei Spalten von $ \mbox{$\bar{U}^\text{t}$}$ den Raum $ \mbox{$V$}$ erzeugen. In anderen Worten, es ist $ \mbox{$x\in\mathbb{C}^n$}$ genau dann in $ \mbox{$V$}$ , wenn die unteren beiden Einträge von $ \mbox{$Ux$}$ verschwinden.

Nun ist $ \mbox{$x\in\mathbb{C}^n$}$ genau dann in $ \mbox{$V^\perp$}$ , wenn für $ \mbox{$v\in V$}$ stets

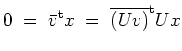
$ \mbox{$\displaystyle 0 \; =\; \bar{v}^\text{t} x \; =\; \overline{(Uv)}^\text{t} Ux $}$
ist. Wir erkennen, daß dies genau dann der Fall ist, wenn die oberen drei Einträge von $ \mbox{$Ux$}$ verschwinden.

Ist nun $ \mbox{$w\in V^\perp$}$ , so wird $ \mbox{$UF'w = DUw$}$ , und da die oberen drei Einträge von $ \mbox{$Uw$}$ verschwinden, gilt dies auch für $ \mbox{$DUw$}$ , und mithin auch für $ \mbox{$UF'w$}$ . Also ist auch $ \mbox{$F'w\in V^\perp$}$ , wie behauptet.

Eine Kernberechnung ergibt eine Basis

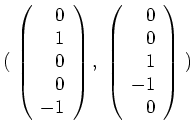
$ \mbox{$\displaystyle (\; \left( \begin{array}{r} 0 \\ 1 \\ 0 \\ 0 \\ ... ...\begin{array}{r} 0 \\ 0 \\ 1 \\ -1 \\ 0 \\ \end{array}\right) \;) $}$
von $ \mbox{$V^\perp$}$ .

Sammeln wir all diese Vektoren ein, so erhalten wir mit

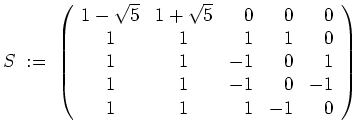
$ \mbox{$\displaystyle S \; :=\; \left( \begin{array}{ccrrr} 1 - \sqrt{5} & 1 +... ...& 1 \\ 1 & 1 & -1 & 0 & -1 \\ 1 & 1 & 1 & -1 & 0 \\ \end{array}\right) $}$
eine invertierbare Matrix, für die
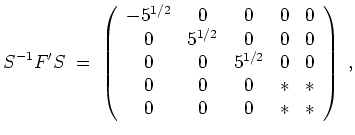
$ \mbox{$\displaystyle S^{-1} F' S \; = \; \left( \begin{array}{ccccc} -5^{1/2... ... & 0 & \ast & \ast \\ 0 & 0 & 0 & \ast & \ast \\ \end{array}\right)\; , $}$
und somit
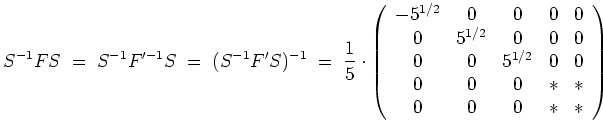
$ \mbox{$\displaystyle S^{-1} F S \; = \; S^{-1} F'^{-1} S\; = \; (S^{-1} F' S)... ... & 0 & 0 & \ast & \ast \\ 0 & 0 & 0 & \ast & \ast \\ \end{array}\right) $}$
ist.

Kann man für allgemeines $ \mbox{$n$}$ eine diagonalisierende Matrix $ \mbox{$S$}$ für $ \mbox{$F$}$ angeben? Die Theorie sagt, daß ein solches $ \mbox{$S$}$ existiert, da $ \mbox{$F$}$ normal ist.