Sei eine ganze Zahl
![]() gegeben. Sei
gegeben. Sei
![]() . Insbesondere ist
. Insbesondere ist
![]() .
.
Unter der diskreten Fouriertransformation versteht man die
![]() -lineare Abbildung
-lineare Abbildung
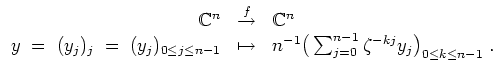
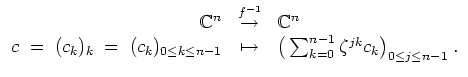
Bei Bedarf sei
![]() und
und
![]() für
für
![]() , i.e. die Vektorindizierung werde
, i.e. die Vektorindizierung werde
![]() -periodisch fortgesetzt.
-periodisch fortgesetzt.
Die Darstellungsmatrix von
![]() bezüglich Standardbasen ist gegeben durch
bezüglich Standardbasen ist gegeben durch
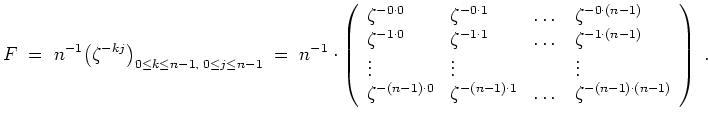
Regeln. Seien
![]() , und schreibe
, und schreibe
![]() und
und
![]() . Seien
. Seien
![]() .
.
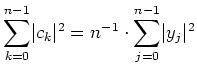 (Parseval).
(Parseval).
Mit der sog. Schnellen Fouriertransformation kann man die Rechengeschwindigkeit für den Fall, daß
![]() eine Potenz von
eine Potenz von
![]() ist (oder jedenfalls durch eine große
ist (oder jedenfalls durch eine große
![]() -Potenz teilbar ist), noch
verbessern. Die resultierende Abbildung ist dieselbe wie bei der gewöhnlich durchgeführten Fouriertransformation.
-Potenz teilbar ist), noch
verbessern. Die resultierende Abbildung ist dieselbe wie bei der gewöhnlich durchgeführten Fouriertransformation.