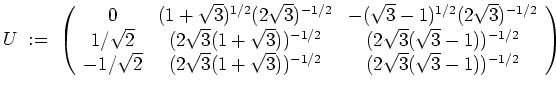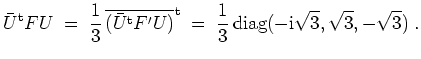Die Beträge der Eigenwerte der unitären Matrix
![]() sind alle gleich
sind alle gleich
![]() . Also sind die Beträge der Eigenwerte von
. Also sind die Beträge der Eigenwerte von
![]() alle gleich
alle gleich
![]() .
.
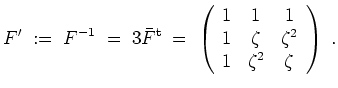
Beachte, daß
![]() , da die Multiplikation mit
, da die Multiplikation mit
![]() diese Summe annulliert, und da
diese Summe annulliert, und da
![]() . Ferner ist
. Ferner ist
![]() .
.
Das charakteristische Polynom ergibt sich zu
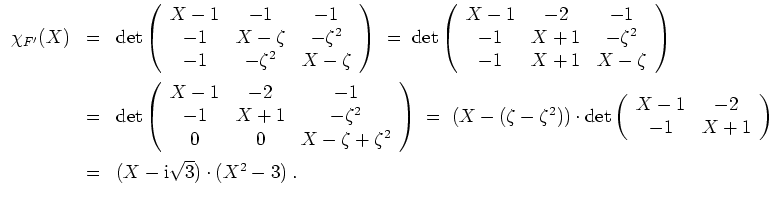
Der Eigenraum von
![]() zum Eigenwert
zum Eigenwert
![]() wird vom Eigenvektor
wird vom Eigenvektor
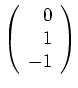 erzeugt.
erzeugt.
Der Eigenraum von
![]() zum Eigenwert
zum Eigenwert
![]() wird vom Eigenvektor
wird vom Eigenvektor
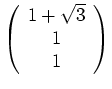 erzeugt.
erzeugt.
Der Eigenraum von
![]() zum Eigenwert
zum Eigenwert
![]() wird vom Eigenvektor
wird vom Eigenvektor
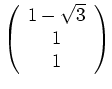 erzeugt.
erzeugt.
Insgesamt wir mit der unitären Matrix