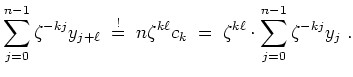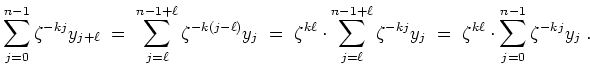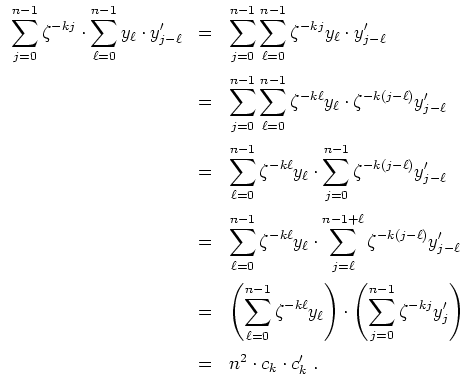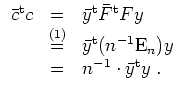Oder aber, wir rechnen direkt. Beachte zunächst, daß aus
![]() folgt, daß
folgt, daß
![]() .
.
Es ist zu zeigen, daß der Eintrag
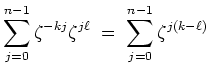
Sei
![]() . Schreibe
. Schreibe
![]() . Es ist
. Es ist
![]() . Ferner wird wegen
. Ferner wird wegen
![]()
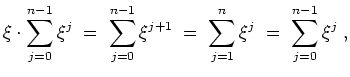
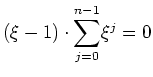 , und folglich
, und folglich
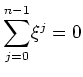 , wie zu zeigen war.
, wie zu zeigen war.
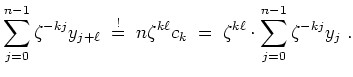
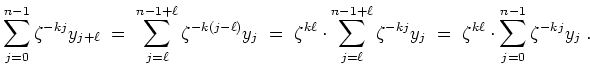
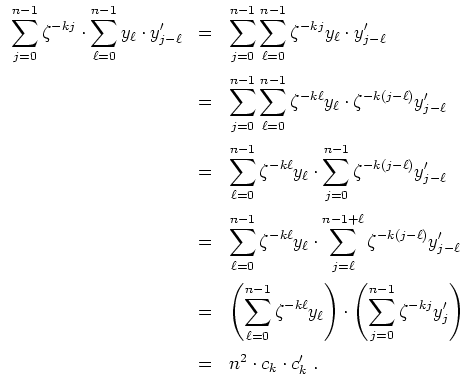
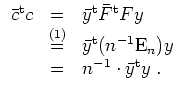
Oder aber, wir rechnen direkt. Beachte zunächst, daß aus
![]() folgt, daß
folgt, daß
![]() .
.
Es ist zu zeigen, daß der Eintrag
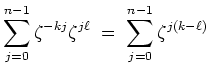
Sei
![]() . Schreibe
. Schreibe
![]() . Es ist
. Es ist
![]() . Ferner wird wegen
. Ferner wird wegen
![]()
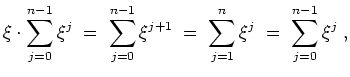
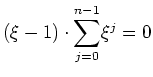 , und folglich
, und folglich
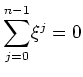 , wie zu zeigen war.
, wie zu zeigen war.