- (1)
- Für
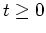 wird
Aus Symmetriegründen wird also
für
wird
Aus Symmetriegründen wird also
für
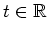 .
.
- (2)
- Es wird
- (3)
- Mit (2) folgt durch Quadrieren
Nun ist aber auch
Ein Vergleich ergibt
für
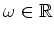 .
.
- (4)
- Die linke Seite der Poissonschen Summationsformel ergibt, unter Verwendung einer geometrischen Reihe,
Die rechte Seite liefert
Ein Vergleich ergibt
wie behauptet.
- (5)
- Die linke Seite der Parsevalschen Gleichung gibt
Die rechte Seite wird zu
Ein Vergleich liefert
wie behauptet.
Das Ergebnis in (5) ergibt sich auch aus dem Residuensatz, denn
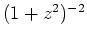 ist in der oberen Halbebene
ist in der oberen Halbebene
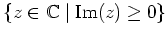 betragsmäßig hinreichend klein für
betragsgroße
betragsmäßig hinreichend klein für
betragsgroße
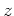 , und hat dort nur bei
, und hat dort nur bei
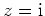 einen Pol, und zwar von Ordnung
einen Pol, und zwar von Ordnung
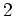 und mit Residuum
und mit Residuum
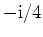 . Als Integralwert erhalten wir somit
. Als Integralwert erhalten wir somit
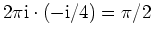 , was unser Ergebnis
bestätigt.
, was unser Ergebnis
bestätigt.
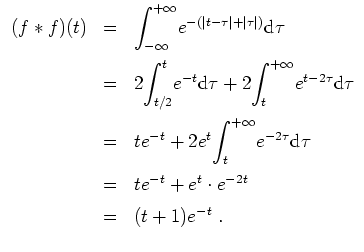
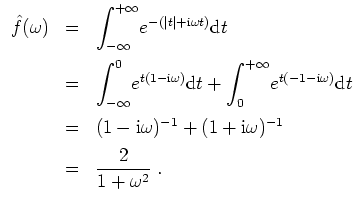
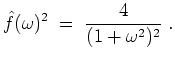
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\hat{f}(\omega)^2
& = & (f\ast f)^\w...
...t}]^\wedge(\omega) + \dfrac{2}{1+\omega^2}\; . \vspace*{2mm} \\
\end{array}$}$](img7.png)
![$ \mbox{$\displaystyle
[\vert t\vert e^{-\vert t\vert}]^\wedge(\omega) \; =\; \dfrac{2(1 - \omega^2)}{(1+\omega^2)^2}
$}$](img8.png)
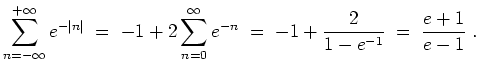
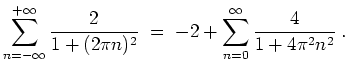
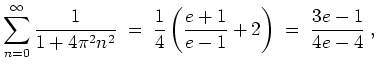
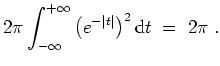
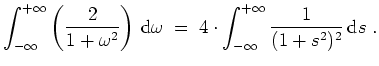
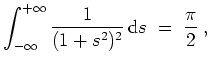
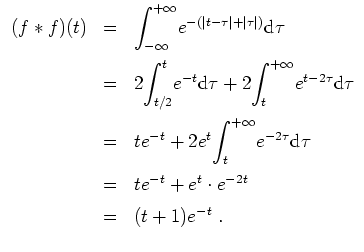
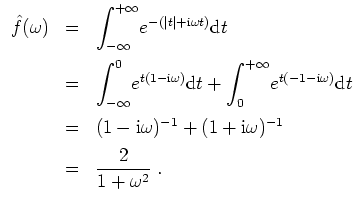
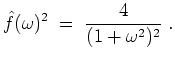
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\hat{f}(\omega)^2
& = & (f\ast f)^\w...
...t}]^\wedge(\omega) + \dfrac{2}{1+\omega^2}\; . \vspace*{2mm} \\
\end{array}$}$](img7.png)
![$ \mbox{$\displaystyle
[\vert t\vert e^{-\vert t\vert}]^\wedge(\omega) \; =\; \dfrac{2(1 - \omega^2)}{(1+\omega^2)^2}
$}$](img8.png)
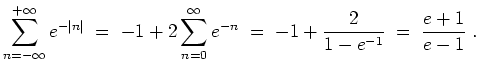
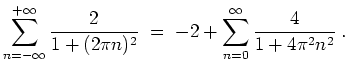
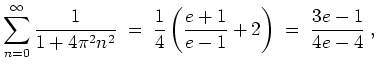
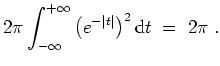
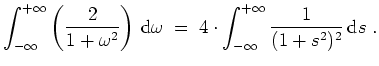
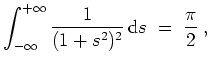
![]() ist in der oberen Halbebene
ist in der oberen Halbebene
![]() betragsmäßig hinreichend klein für
betragsgroße
betragsmäßig hinreichend klein für
betragsgroße
![]() , und hat dort nur bei
, und hat dort nur bei
![]() einen Pol, und zwar von Ordnung
einen Pol, und zwar von Ordnung
![]() und mit Residuum
und mit Residuum
![]() . Als Integralwert erhalten wir somit
. Als Integralwert erhalten wir somit
![]() , was unser Ergebnis
bestätigt.
, was unser Ergebnis
bestätigt.