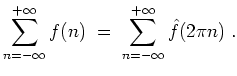Definition.
Sei
![]() so gegeben, daß
so gegeben, daß
![]() für alle
für alle
![]() von
von
![]() bis
bis
![]() integrierbar ist. Es heiße diesenfalls
integrierbar ist. Es heiße diesenfalls
![]() fouriertransformierbar, und die resultierende Funktion
fouriertransformierbar, und die resultierende Funktion
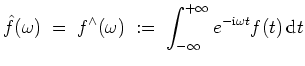
Wir erlauben uns bei Bedarf auch,
![]() zu schreiben. Das Argument
zu schreiben. Das Argument
![]() diene hierbei nur der Kenntlichmachung der fourierzutransformierenden Funktion, das
Resultat ist weiterhin eine Funktion in
diene hierbei nur der Kenntlichmachung der fourierzutransformierenden Funktion, das
Resultat ist weiterhin eine Funktion in
![]() .
.
Ist
![]() stückweise stetig und ist
stückweise stetig und ist
![]() von
von
![]() bis
bis
![]() integrierbar ist, so heiße
integrierbar ist, so heiße
![]() absolut integrierbar. Absolut integrierbare Funktionen sind fouriertransformierbar.
absolut integrierbar. Absolut integrierbare Funktionen sind fouriertransformierbar.
Regeln.
Seien
![]() fouriertransformierbar. Seien
fouriertransformierbar. Seien
![]() . Sei
. Sei
![]() . Sei
. Sei
![]() ganz.
ganz.
Folgende Gleichheiten gelten für alle
![]() .
.
![$ \mbox{$[\overline{f(t)}]^\wedge(\omega) = \overline{\hat{f}(-\omega)}$}$](img19.png) .
.
Ist
![]() hingegen nur stückweise stetig differenzierbar, und existieren an jeder Sprungstelle die einseitigen Grenzwerte von
hingegen nur stückweise stetig differenzierbar, und existieren an jeder Sprungstelle die einseitigen Grenzwerte von
![]() und von
und von
![]() , so gilt die Formel weiterhin, mit der
Modifikation, daß an den Sprungstellen von
, so gilt die Formel weiterhin, mit der
Modifikation, daß an den Sprungstellen von
![]() die Funktion
die Funktion
![]() den (arithmetischen) Mittelwert der einseitigen Grenzwerte von
den (arithmetischen) Mittelwert der einseitigen Grenzwerte von
![]() als Wert annimmt.
als Wert annimmt.
Sei erwähnt, daß bei Fouriertransformationen in der Praxis häufig mit verallgemeinerten Funktionen, sogenannten Distributionen, gerechnet wird. So etwa ist die
Fouriertransformierte der konstanten Funktion
![]() das
das
![]() -fache des Diracschen
-fache des Diracschen
![]() . Wir wollen uns dagegen auf Funktionen im eigentlichen Sinne beschränken.
. Wir wollen uns dagegen auf Funktionen im eigentlichen Sinne beschränken.
Faltung.
Seien
![]() absolut integrierbar. Sei die Funktion
absolut integrierbar. Sei die Funktion
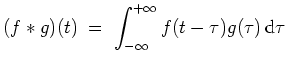
Dann ist
Parseval.
Ist
![]() absolut integrierbar, so gilt die Parsevalsche (Norm-)Gleichung
absolut integrierbar, so gilt die Parsevalsche (Norm-)Gleichung
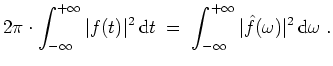
Poisson.
Ist
![]() absolut integrierbar, so gilt die Poissonsche Summationsformel
absolut integrierbar, so gilt die Poissonsche Summationsformel