Sei
![]() . Setze
. Setze
![]() für
für
![]() . Die Poissonsche Summationsformel gibt
. Die Poissonsche Summationsformel gibt
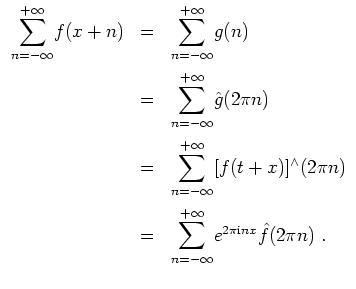
Die erhaltene Formel besagt, daß der Wert der Fouriertransformierten bei
![]() gerade der
gerade der
![]() -te Koeffizient der komplexen Fourierentwicklung der ''Periodifizierung''
-te Koeffizient der komplexen Fourierentwicklung der ''Periodifizierung''
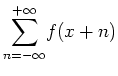 von
von
![]() ist.
ist.