Lösung.

1.
Wir erhalten für $ \mbox{$k\ne 0$}$
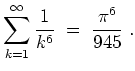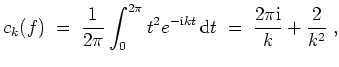
$ \mbox{$\displaystyle c_k(f) \;=\; \frac{1}{2\pi} \int_0^{2\pi} t^2 e^{-\mathrm{i}kt}\,\text{d}t \;=\; \frac{2\pi\mathrm{i}}{k} + \frac{2}{k^2}\; , $}$
sowie
$ \mbox{$\displaystyle c_0(f) = \frac{1}{2\pi} \int_0^{2\pi} t^2 \,\text{d}t = \frac{4\pi^2}{3} $}$
und somit
$ \mbox{$\displaystyle \text{S}_f(x) \;=\; \frac{4\pi^2}{3} + \sum_{k = -\infty... ...left(\frac{2\pi\mathrm{i}}{k} + \frac{2}{k^2}\right)\; e^{\mathrm{i}kx} \; . $}$

Skizze des Graphen der ersten $ \mbox{$4$}$ und des Graphen der ersten $ \mbox{$40$}$ Summanden der zugehörigen reellen Fourierreihe

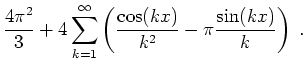
$ \mbox{$\displaystyle \frac{4\pi^2}{3} + 4\sum_{k = 1}^\infty \left(\frac{\cos(kx)}{k^2} - \pi \frac{\sin(kx)}{k}\right)\; . $}$
\includegraphics[width = 12cm]{quad_per.eps}

2.
Wir erhalten für $ \mbox{$k\ne 0$}$
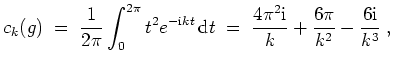
$ \mbox{$\displaystyle c_k(g) \;=\; \frac{1}{2\pi} \int_0^{2\pi} t^2 e^{-\mathr... ... \frac{4\pi^2\mathrm{i}}{k} + \frac{6\pi}{k^2} - \frac{6\mathrm{i}}{k^3}\; , $}$
sowie
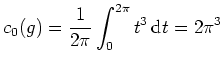
$ \mbox{$\displaystyle c_0(g) = \frac{1}{2\pi} \int_0^{2\pi} t^3 \,\text{d}t = 2\pi^3 $}$
und somit
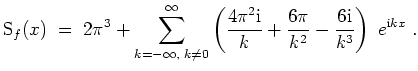
$ \mbox{$\displaystyle \text{S}_f(x) \;=\; 2\pi^3 + \sum_{k = -\infty,\; k\ne 0... ... + \frac{6\pi}{k^2} - \frac{6\mathrm{i}}{k^3}\right)\; e^{\mathrm{i}kx} \; . $}$

Skizze des Graphen der ersten $ \mbox{$4$}$ und des Graphen der ersten $ \mbox{$40$}$ Summanden der zugehörigen reellen Fourierreihe

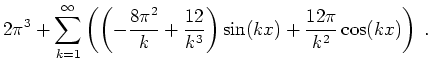
$ \mbox{$\displaystyle 2\pi^3 + \sum_{k = 1}^\infty \left(\left(-\frac{8\pi^2}{k} + \frac{12}{k^3}\right)\sin(kx) + \frac{12\pi}{k^2}\cos(kx)\right) \; . $}$
\includegraphics[width = 12cm]{cube_per.eps}

3.
Die Parsevalsche Skalarproduktgleichung ergibt für $ \mbox{$f$}$ und $ \mbox{$g$}$
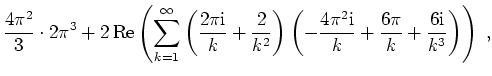
$ \mbox{$\displaystyle \frac{4\pi^2}{3}\cdot 2\pi^3 + 2\,\text{Re}\left(\sum_{k... ...\mathrm{i}}{k} + \frac{6\pi}{k} + \frac{6\mathrm{i}}{k^3}\right)\right) \; , $}$
also
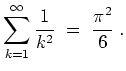
$ \mbox{$\displaystyle \sum_{k = 1}^\infty \frac{1}{k^2} \;=\; \frac{\pi^2}{6}\; . $}$

Die Parsevalsche Normgleichung ergibt für $ \mbox{$f$}$

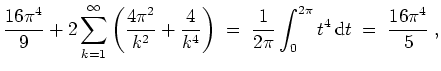
$ \mbox{$\displaystyle \frac{16\pi^4}{9} + 2\sum_{k = 1}^\infty\left(\frac{4\pi... ...\;=\; \frac{1}{2\pi}\int_0^{2\pi} t^4\,\text{d}t \;=\; \frac{16\pi^4}{5}\; , $}$
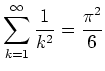also, unter Verwendung von $ \mbox{$\displaystyle\sum_{k = 1}^\infty \frac{1}{k^2} = \frac{\pi^2}{6}$}$ ,
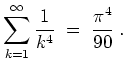
$ \mbox{$\displaystyle \sum_{k = 1}^\infty \frac{1}{k^4} \;=\; \frac{\pi^4}{90}\; . $}$

Die Parsevalschen Normgleichung ergibt für $ \mbox{$g$}$

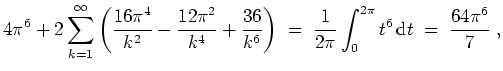
$ \mbox{$\displaystyle 4\pi^6 + 2\sum_{k = 1}^\infty\left(\frac{16\pi^4}{k^2} -... ...;=\; \frac{1}{2\pi}\int_0^{2\pi} t^6\,\text{d}t \;=\; \frac{64\pi^6}{7}\; , $}$
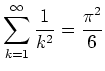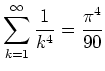also, unter Verwendung von $ \mbox{$\displaystyle\sum_{k = 1}^\infty \frac{1}{k^2} = \frac{\pi^2}{6}$}$ und von $ \mbox{$\displaystyle\sum_{k = 1}^\infty \frac{1}{k^4} = \frac{\pi^4}{90}$}$ ,
$ \mbox{$\displaystyle \sum_{k = 1}^\infty \frac{1}{k^6} \;=\; \frac{\pi^6}{945}\; . $}$