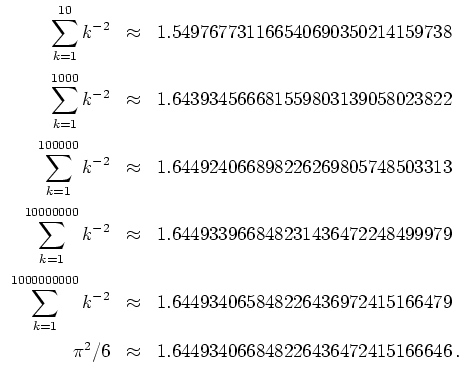
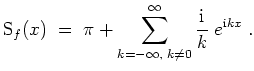
Skizze des Graphen der ersten
![]() und des Graphen der ersten
und des Graphen der ersten
![]() Summanden der zugehörigen reellen Fourierreihe
Summanden der zugehörigen reellen Fourierreihe
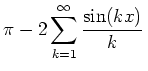 .
.
![\includegraphics[width = 12cm, height = 8cm]{saege.eps}](img8.png)
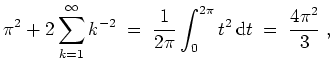
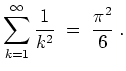
Zum Vergleich, es sind
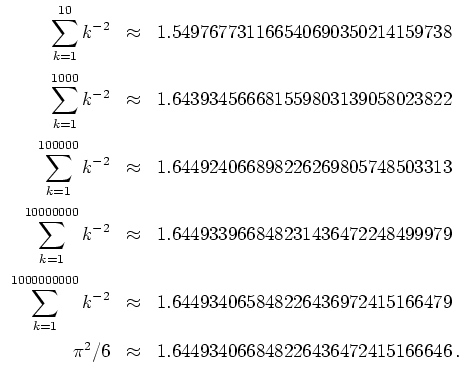
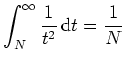
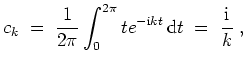
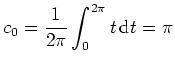
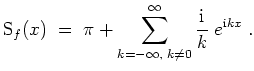
Skizze des Graphen der ersten
![]() und des Graphen der ersten
und des Graphen der ersten
![]() Summanden der zugehörigen reellen Fourierreihe
Summanden der zugehörigen reellen Fourierreihe
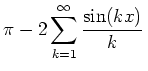 .
.
![\includegraphics[width = 12cm, height = 8cm]{saege.eps}](img8.png)
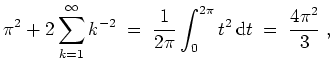
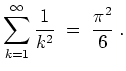
Zum Vergleich, es sind