Lösung.

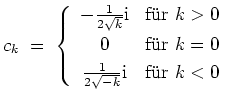
Wäre die angegebene Reihe eine Funktion wie angegeben, so wäre

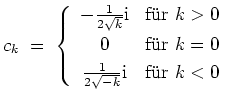
$ \mbox{$\displaystyle c_k \;=\; \left\{ \begin{array}{cl} -\frac{1}{2\sqrt k}... ...2\sqrt{-k}}\mathrm{i}& \text{f\uml ur {$\mbox{$k < 0$}$}} \end{array}\right. $}$
die Koeffizientenfolge $ \mbox{$(c_k)_{k\in\mathbb{Z}}$}$ der Fourierentwicklung einer stetigen Funktion.

Mit der Parsevalschen Normgleichung gäbe das die konvergente Reihe

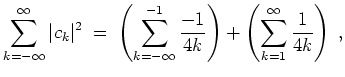
$ \mbox{$\displaystyle \sum_{k = -\infty}^{\infty} \vert c_k\vert^2 \;=\; \left... ...\frac{-1}{4k} \right) + \left(\sum_{k = 1}^{\infty} \frac{1}{4k} \right)\; , $}$
welche aber in beiden Bestandteilen divergiert. Das gibt uns einen Widerspruch.

Skizze des Graphen der ersten $ \mbox{$5$}$ und des Graphen der ersten $ \mbox{$100$}$ Summanden der angegebenen trigonometrischen Reihe.

\includegraphics[width = 12cm]{l1_par.eps}