Lösung.

1.
Die Funktion ist ungerade, daher ist stets $ \mbox{$a_k = 0\,$}$ .

Die Funktionswerte von $ \mbox{$f$}$ in $ \mbox{$\{0,\pi\}$}$ spielen für die Berechnung der Koeffizienten $ \mbox{$b_k$}$ keine Rolle. Wir erhalten für $ \mbox{$k\geq 1$}$

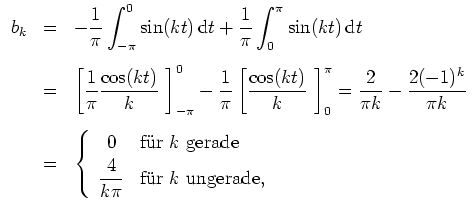
$ \mbox{$\displaystyle \begin{array}{rcl} b_k & = & -\dfrac{1}{\pi}\display... ...ext{f\uml ur {$\mbox{$k$}$} ungerade,}\\ \end{array}\right. \end{array} $}$
woraus sich die Fourierreihe
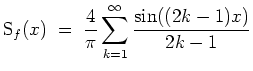
$ \mbox{$\displaystyle \text{S}_f(x) \;=\; \frac{4}{\pi}\sum_{k=1}^\infty\frac{\sin((2k-1)x)}{2k-1} $}$
ergibt.

In $ \mbox{$(-\pi,0)\cup (0,\pi)$}$ ist $ \mbox{$f$}$ differenzierbar, dort ist also $ \mbox{$\text{S}_f(x) = f(x)$}$ .

Ist $ \mbox{$x\in\pi\mathbb{Z}$}$ , so hat $ \mbox{$f$}$ in $ \mbox{$x$}$ einen links- und rechtsseitigen Grenzwert, und ist links- und rechtsseitig differenzierbar. Als Wert der Fourierreihe ergibt sich das arithmetische Mittel des linksseitigen und des rechtsseitigen Grenzwerts, nämlich $ \mbox{$0$}$ . Dies ist zugleich der Funktionswert von $ \mbox{$f$}$ in $ \mbox{$x$}$ . Also ist auch hier $ \mbox{$\text{S}_f(x) = f(x)$}$ .

Insgesamt ist $ \mbox{$\text{S}_f(x) = f(x)$}$ für alle $ \mbox{$x\in\mathbb{R}$}$ .

Skizze des Graphen der ersten $ \mbox{$3$}$ und des Graphen der ersten $ \mbox{$20$}$ Summanden der Fourierreihe.

\includegraphics[width = 12cm]{s2_1.eps}

Skizze des Graphen der ersten $ \mbox{$1000$}$ Summanden der Fourierreihe in der Nähe von $ \mbox{$x = 0$}$ .

\includegraphics[width = 12cm]{s2_2.eps}

2.
Die Funktion $ \mbox{$g$}$ ist auf $ \mbox{$(-\pi,\pi)$}$ bis auf die Ausnahmestelle $ \mbox{$0$}$ stetig differenzierbar, also gilt dort $ \mbox{$g'=f\,$}$ . An der Ausnahmestelle $ \mbox{$0$}$ ist $ \mbox{$g$}$ stetig und besitzt eine links- und rechtsseitige Ableitung, nämlich $ \mbox{$-1$}$ und $ \mbox{$1$}$ , deren Mittelwert gerade $ \mbox{$0=f(0)$}$ ist. Also erhalten wir durch summandenweises Aufleiten
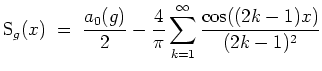
$ \mbox{$\displaystyle \text{S}_g(x) \;=\; \frac{a_0(g)}{2} - \frac{4}{\pi}\sum_{k=1}^\infty\frac{\cos((2k-1)x)}{(2k-1)^2} $}$
mit
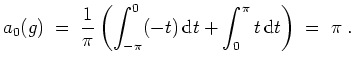
$ \mbox{$\displaystyle a_0(g) \;=\; \frac{1}{\pi}\left(\int_{-\pi}^0 (-t)\,\text{d}t + \int_0^{\pi} t\,\text{d}t\right) \;=\; \pi \; . $}$
Insgesamt wird also
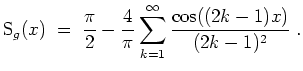
$ \mbox{$\displaystyle \text{S}_g(x) \;=\; \frac{\pi}{2} - \frac{4}{\pi}\sum_{k=1}^\infty\frac{\cos((2k-1)x)}{(2k-1)^2}\; . $}$

Skizze des Graphen der ersten $ \mbox{$2$}$ und des Graphen der ersten $ \mbox{$10$}$ Summanden der Fourierreihe.

\includegraphics[width = 12cm]{s2_3.eps}

Skizze des Graphen der ersten $ \mbox{$40$}$ und des Graphen der ersten $ \mbox{$800$}$ Summanden der Fourierreihe in der Nähe von $ \mbox{$x = 0$}$ .

\includegraphics[width = 12cm]{s2_4.eps}