Es ist
also reell und folglich gilt
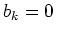 .
.
Ferner ist
und somit
Die Funktion
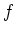 ist auf
ist auf
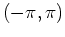 differenzierbar, und bei
differenzierbar, und bei
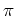 stetig und rechts- wie linksseitig differenzierbar. Somit folgt
stetig und rechts- wie linksseitig differenzierbar. Somit folgt
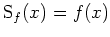 für alle
für alle
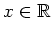 .
.
Skizze des Graphen der ersten
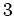 und des Graphen der ersten
und des Graphen der ersten
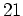 Summanden der Fourierreihe.
Summanden der Fourierreihe.
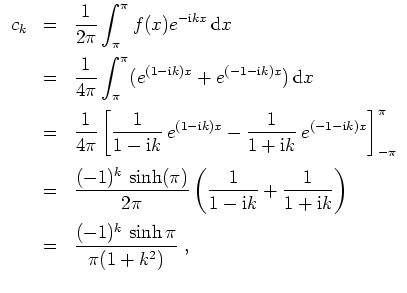
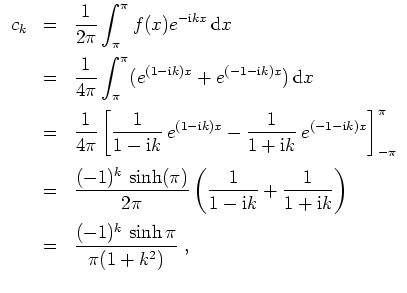
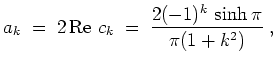
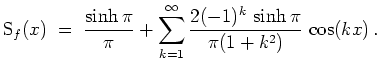
![]() und des Graphen der ersten
und des Graphen der ersten
![]() Summanden der Fourierreihe.
Summanden der Fourierreihe.
![\includegraphics[width = 12cm]{s1.eps}](img12.png)