Fourierentwicklung.

Periodische Funktionen.

Eine Funktion $ \mbox{$f:\mathbb{R}\to \mathbb{C}$}$ heißt periodisch mit Periode $ \mbox{$p>0$}$ , falls sie auf ganz $ \mbox{$\mathbb{R}$}$ die Identität

$ \mbox{$\displaystyle f(x+p)=f(x) $}$
erfüllt. Die einfachsten periodischen Funktionen sind
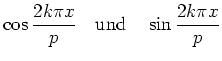
$ \mbox{$\displaystyle \cos{\frac{2k\pi x}{p}}\quad\text{und}\quad\sin{\frac{2k\pi x}{p}} $}$
sowie
$ \mbox{$\displaystyle e^{2k\pi \text{i}x/p} $}$
für $ \mbox{$k\in\mathbb{Z}$}$ .

$ \mbox{$\mathbb{C}$}$ -Linearkombinationen periodischer Funktionen sind periodisch.

Trigonometrische Polynome.

Eine Funktion $ \mbox{$f:\mathbb{R}\to \mathbb{C}$}$ der Gestalt

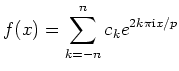
$ \mbox{$\displaystyle f(x)=\sum_{k=-n}^n{c_k e^{2k\pi \text{i}x/p}} $}$
mit $ \mbox{$p>0$}$ , $ \mbox{$n\in\mathbb{N}$}$ und $ \mbox{$c_{-n},\dots,c_n\in\mathbb{C}$}$ nennt man ( $ \mbox{$p$}$ -periodisches) trigonometrisches Polynom.

Setzt man für $ \mbox{$k\ge 0$}$

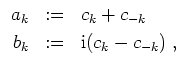
$ \mbox{$\displaystyle \begin{array}{rcl} a_k & := & c_k+c_{-k} \vspace{1mm}\\ b_k & := & \mathrm{i}(c_k-c_{-k}) \; , \\ \end{array} $}$
so ist $ \mbox{$b_0 = 0$}$ und
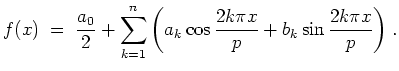
$ \mbox{$\displaystyle f(x)\; =\; \frac{a_0}{2}+\sum_{k=1}^n{\left(a_k\cos{\frac{2k\pi x}{p}}+b_k\sin{\frac{2k\pi x}{p}}\right)}\; . $}$

Umgekehrt erhält man für $ \mbox{$k\ge 0$}$ aus den Koeffizienten $ \mbox{$a_k$}$ und $ \mbox{$b_k$}$ die Koeffizienten $ \mbox{$c_k$}$ durch

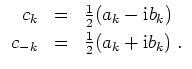
$ \mbox{$\displaystyle \begin{array}{rcl} c_k &=& \frac{1}{2}(a_k-\mathrm{i}b... ...{1mm}\\ c_{-k} &=& \frac{1}{2}(a_k+\mathrm{i}b_k) \; . \\ \end{array} $}$
zurück.

Beachte, daß alle Koeffizienten $ \mbox{$a_k$}$ , $ \mbox{$b_k$}$ genau dann reell sind, wenn stets $ \mbox{$c_{-k} = \overline{c_k}$}$ gilt.

Trigonometrische Reihen

Eine trigonometrische Reihe mit Periode $ \mbox{$p>0$}$ ist eine Funktionenreihe der Gestalt

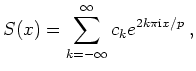
$ \mbox{$\displaystyle S(x)=\sum_{k=-\infty}^{\infty}{c_k e^{2k\pi \text{i}x/p}}\; , $}$
mit $ \mbox{$c_k\in\mathbb{C}$}$ , welche gemäß den obigen Umrechnungsregeln auch als
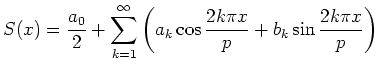
$ \mbox{$\displaystyle S(x)=\frac{a_0}{2}+\sum_{k=1}^\infty{\left(a_k\cos{\frac{2k\pi x}{p}}+b_k\sin{\frac{2k\pi x}{p}}\right)} $}$
geschrieben werden kann.

Eine trigonometrische Reihe kann konvergieren oder divergieren.

Fourierkoeffizienten und Fourierreihen.

Es sei $ \mbox{$p > 0\,$}$ und $ \mbox{$f:\mathbb{R}\to \mathbb{C}\,$}$ eine $ \mbox{$p$}$ -periodische, über $ \mbox{$[0,p]\,$}$ integrierbare Funktion. Die Fourierkoeffizienten von $ \mbox{$f$}$ sind folgendermaßen gegeben.

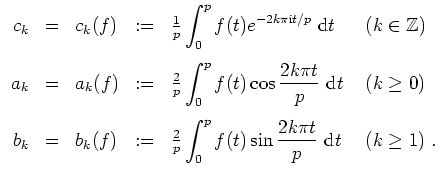
$ \mbox{$\displaystyle \begin{array}{rclcll} c_k & = & c_k(f) & := &\frac{1}{... ...{f(t)\sin{\frac{2k\pi t}{p}}\ \text{d}t} &\ (k\ge 1) \; . \\ \end{array} $}$
Wegen der $ \mbox{$p$}$ -Periodizität können die auftretenden Integrale auch über jedem beliebigen Intervall der Länge $ \mbox{$p\,$}$ berechnet werden.

Dann hängen die Koeffizienten $ \mbox{$a_k$}$ , $ \mbox{$b_k\,$}$ und $ \mbox{$c_k\,$}$ wie oben beschrieben zusammen.

Ist die Funktion $ \mbox{$f$}$ auf $ \mbox{$[-\frac{p}{2},\frac{p}{2}]$}$ eine bis auf endlich viele Ausnahmestellen gerade Funktion, oder allgemeiner, ist dort fast überall $ \mbox{$f(x) = f(-x)$}$ , so gilt $ \mbox{$b_k(f)=0$}$ für alle $ \mbox{$k\ge 1$}$ .

Ist die Funktion $ \mbox{$f$}$ auf $ \mbox{$[-\frac{p}{2},\frac{p}{2}]$}$ eine bis auf endlich viele Ausnahmestellen ungerade Funktion, oder allgemeiner, ist dort fast überall $ \mbox{$f(x) = -f(-x)$}$ , so gilt $ \mbox{$a_k(f)=0$}$ für alle $ \mbox{$k\ge 0$}$ .

Die Fourierreihe oder Fourierentwicklung von $ \mbox{$f$}$ ist gegeben durch

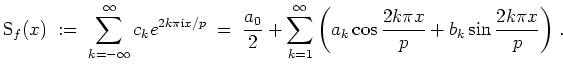
$ \mbox{$\displaystyle \text{S}_f(x) \; :=\; \sum_{k=-\infty}^{\infty}{c_k e^{... ...ty{\left(a_k\cos{\frac{2k\pi x}{p}}+b_k\sin{\frac{2k\pi x}{p}}\right)} \; . $}$

Konvergenz von Fourierreihen.

Sei $ \mbox{$f:\mathbb{R}\to \mathbb{C}$}$ $ \mbox{$p$}$ -periodisch und integrierbar über $ \mbox{$[0,p]$}$ . Gilt für $ \mbox{$x\in\mathbb{R}$}$ , daß dort

(i)
$ \mbox{$f(x+)$}$ und $ \mbox{$f(x-)$}$ existieren (d.h. einseitige Grenzwerte existieren), und
(ii)
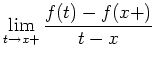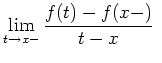$ \mbox{$\lim\limits_{t\to x+}{\dfrac{f(t)-f(x+)}{t-x}}\ $}$ und $ \mbox{$\lim\limits_{t\to x-}{\dfrac{f(t)-f(x-)}{t-x}}\ $}$ existieren (d.h. einseitige Ableitungen existieren),
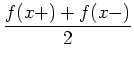so konvergiert die Fourierreihe von $ \mbox{$f$}$ bei $ \mbox{$x$}$ gegen $ \mbox{$\dfrac{f(x+)+f(x-)}{2}$}$ .

Anschaulich gesprochen, hat $ \mbox{$f$}$ bei $ \mbox{$x$}$ eine Tangente von links und eine Tangente von rechts, so ist der Wert der Fourierreihe bei $ \mbox{$x$}$ genau der Mittelwert des links- und rechtsseitigen Funktionswertes von $ \mbox{$f$}$ an dieser Stelle.

Insbesondere, ist $ \mbox{$f$}$ bei $ \mbox{$x$}$ differenzierbar, so ist $ \mbox{$\text{S}_f(x) = f(x)$}$ . Das ist der Regelfall.

Allgemeiner, auch wenn $ \mbox{$f$}$ bei $ \mbox{$x$}$ stetig und links- wie rechtsseitig differenzierbar ist, so gilt dort $ \mbox{$\text{S}_f(x) = f(x)$}$ .

Anschaulich, hat $ \mbox{$f$}$ bei $ \mbox{$x$}$ einen Knick, aber sowohl links- wie rechtsseitig eine Tangente, so hat die Fourierreihe dort trotzdem den selben Funktionswert wie $ \mbox{$f$}$ .

Der reelle Fall.

Ist $ \mbox{$f$}$ wie oben, nur reellwertig, so ist stets $ \mbox{$c_{-k} = \overline{c_k}$}$ , und folglich

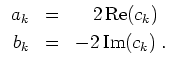
$ \mbox{$\displaystyle \begin{array}{rcr} a_k & = & 2\,\text{Re}(c_k) \;\, \vspace{1mm}\\ b_k & = & -2\,\text{Im}(c_k) \; . \\ \end{array} $}$

Summandenweises Ableiten.

Es sei $ \mbox{$f:\mathbb{R}\to \mathbb{C}$}$ $ \mbox{$p$}$ -periodisch, auf $ \mbox{$(-p,p)$}$ stetig differenzierbar bis auf endlich viele Ausnahmestellen und an diesen Ausnahmestellen noch stetig.

Sei $ \mbox{$f'$}$ die $ \mbox{$p$}$ -periodische Funktion, die außer an den Ausnahmestellen die Ableitung von $ \mbox{$f$}$ darstellt, und die an einer Ausnahmestelle $ \mbox{$x_0$}$ den Wert $ \mbox{$(\lim\limits_{x\to x_0+} f'(x) + \lim\limits_{x\to x_0-} f'(x))/2$}$ annimmt, so erhalten wir durch summandenweises Differenzieren

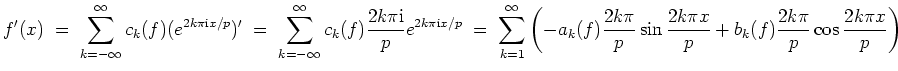
$ \mbox{$\displaystyle f'(x) \;=\; \sum_{k = -\infty}^{\infty} c_k(f) (e^{2k\p... ...n{\frac{2k\pi x}{p}} + b_k(f)\frac{2k\pi}{p}\cos{\frac{2k\pi x}{p}}\right)} $}$
für alle $ \mbox{$x\in\mathbb{R}$}$ .

Kennt man umgekehrt die Fourierreihe zu $ \mbox{$f'$}$ und möchte auf die Fourierreihe von $ \mbox{$f$}$ schließen, wobei $ \mbox{$f$}$ die ebengenannten Bedingungen erfüllt, so genügt es, $ \mbox{$c_0(f)$}$ zu berechnen.