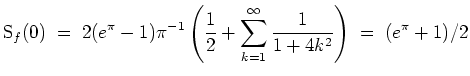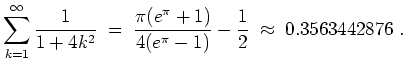Eine direkte Berechnung der reellen Fourierkoeffizienten wäre aufwendiger als die nun durchzuführende Berechnung der
komplexen Fourierkoeffizienten von
![]() . Es ist
. Es ist
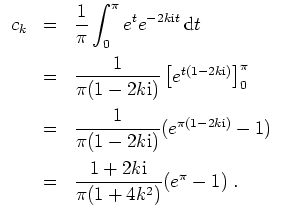
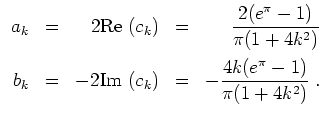
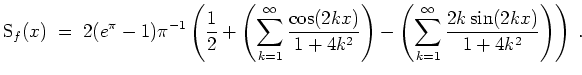
Skizze des Graphen der jeweils ersten
![]() und des Graphen der jeweils ersten
und des Graphen der jeweils ersten
![]() Summanden der Fourierreihe.
Summanden der Fourierreihe.
![\includegraphics[width = 12cm]{l3.eps}](img8.png)
Da
![]() für
für
![]() differenzierbar ist, gilt dort
differenzierbar ist, gilt dort
![]() .
.
Bei
![]() ist
ist
![]() noch einseitig stetig und einseitig differenzierbar mit
noch einseitig stetig und einseitig differenzierbar mit
![]() und
und
![]() . Also gilt dort
. Also gilt dort