Lösung.

Reelle Berechnung der Fourierkoeffizienten.

Es ist $ \mbox{$f$}$ auf $ \mbox{$[-\pi,\pi]$}$ eine ungerade Funktion, außer bei $ \mbox{$x = 0$}$ . Also ist $ \mbox{$a_k = 0$}$ für alle $ \mbox{$k\ge 0$}$ .

Wir berechnen noch

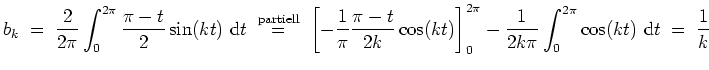
$ \mbox{$\displaystyle b_k\; =\;\frac{2}{2\pi}\displaystyle\int_0^{2\pi}{\frac... ...{1}{2k\pi}\displaystyle\int_0^{2\pi}{\cos(kt)\ \text{d}t}\; =\;\frac{1}{k} $}$
für $ \mbox{$k\geq 1$}$ , also ist die Fourierreihe von $ \mbox{$f$}$ gegeben durch
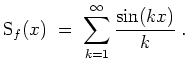
$ \mbox{$\displaystyle \text{S}_f(x) \;=\; \sum_{k=1}^\infty {\frac{\sin(kx)}{k}}\; . $}$

Komplexe Berechnung der Fourierkoeffizienten.

Wir erhalten für $ \mbox{$k\in\mathbb{Z}\setminus \{ 0\}$}$ durch partielle Integration

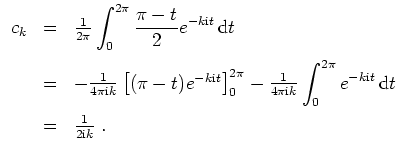
$ \mbox{$\displaystyle \begin{array}{rcl} c_k & = & \frac{1}{2\pi}\displayst... ...t{d}t \vspace*{2mm}\\ & = & \frac{1}{2\mathrm{i}k}\; . \\ \end{array} $}$
Für $ \mbox{$k = 0$}$ erhalten wir
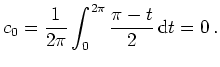
$ \mbox{$\displaystyle c_0 = \frac{1}{2\pi}\int_0^{2\pi}\frac{\pi-t}{2}\,\text{d}t = 0\,. $}$
Insbesondere sind $ \mbox{$a_k = c_k + c_{-k} = 0$}$ und $ \mbox{$b_k = \mathrm{i}(c_k - c_{-k}) = \frac{1}{k}\,$}$ , und wir erhalten erneut
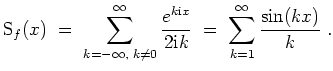
$ \mbox{$\displaystyle \text{S}_f(x) \;=\; \sum_{k = -\infty,\; k\ne 0}^{\inft... ...mathrm{i}x}}{2\mathrm{i}k} \; =\; \sum_{k=1}^\infty{\frac{\sin(kx)}{k}}\; . $}$

Skizze des Graphen der ersten $ \mbox{$4$}$ und des Graphen der ersten $ \mbox{$20$}$ Summanden der Fourierreihe.

\includegraphics[width = 12cm]{l1.eps}

Da $ \mbox{$f(x)$}$ für $ \mbox{$x\in (0,2\pi)$}$ differenzierbar ist, gilt dort $ \mbox{$f(x) = \text{S}_f(x)$}$ .

Da $ \mbox{$f$}$ in $ \mbox{$x = 0$}$ links- wie rechtsseitig einen Grenzwert besitzt, nämlich $ \mbox{$f(0-) = -\frac{\pi}{2}$}$ und $ \mbox{$f(0+) = \frac{\pi}{2}$}$ , und dort auch links- und rechtsseitig differenzierbar ist, gilt dort $ \mbox{$\text{S}_f(x) = (f(0+) + f(0-))/2 = 0\,$}$ .