- Der Rand von
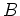 setzt sich aus dem Kreis in der
setzt sich aus dem Kreis in der
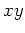 -Ebene mit Radius 2 um den Nullpunkt und dem Paraboloid
-Ebene mit Radius 2 um den Nullpunkt und dem Paraboloid
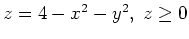 , zusammen. Wir parametrisieren also
sowie
Die unterschiedliche Wahl der ersten Komponenten mag zunächst ungewöhnlich erscheinen, ist jedoch dadurch bedingt,
daß wir garantieren möchten, daß die folgenden Normalenvektoren der Flächen
, zusammen. Wir parametrisieren also
sowie
Die unterschiedliche Wahl der ersten Komponenten mag zunächst ungewöhnlich erscheinen, ist jedoch dadurch bedingt,
daß wir garantieren möchten, daß die folgenden Normalenvektoren der Flächen
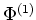 und
und
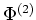 jeweils nach
außen zeigen.
Nun ist
Folglich berechnen wir
und
Wir haben also berechnet, daß
jeweils nach
außen zeigen.
Nun ist
Folglich berechnen wir
und
Wir haben also berechnet, daß
- Wir bemerken, daß die Voraussetzungen des Gaußschen Integralsatzes erfüllt sind und bestimmen
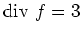 .
Unter Verwendung von Zylinderkoordinaten ist
.
Unter Verwendung von Zylinderkoordinaten ist
![$ \mbox{$\displaystyle
\Phi^{(1)}: \underbrace{[0,2] \times [0,2\pi]}_{=:\; K^{...
...rphi) := \begin{pmatrix}r \sin \varphi\\ r \cos \varphi\\ 0 \end{pmatrix},
$}$](img4.png)
![$ \mbox{$\displaystyle
\Phi^{(2)}: \underbrace{[0,2] \times [0,2\pi]}_{=:\; K^{...
...) := \begin{pmatrix}r \cos \varphi\\ r \sin \varphi\\ 4-r^2 \end{pmatrix}.
$}$](img5.png)
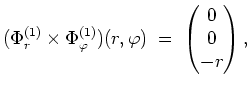
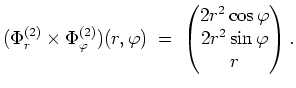
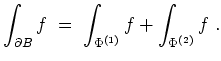
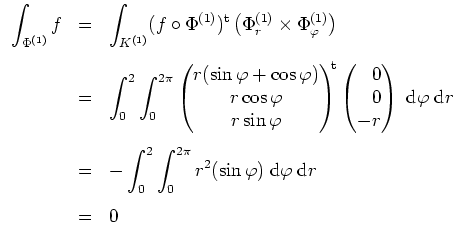
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle \int_{\Phi^{(2)}} f
&=&...
...dfrac{r^4}{4} + 2r^2 \right]_0^2 \vspace{3mm}\\
&=& 24 \pi \; .
\end{array}$}$](img12.png)
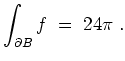
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle \int_{\partial B} f
&=...
...2r^2 - \dfrac{r^4}{4} \right]_0^2\vspace{3mm}\\
&=& 24 \pi \; .
\end{array}$}$](img15.png)
![$ \mbox{$\displaystyle
\Phi^{(1)}: \underbrace{[0,2] \times [0,2\pi]}_{=:\; K^{...
...rphi) := \begin{pmatrix}r \sin \varphi\\ r \cos \varphi\\ 0 \end{pmatrix},
$}$](img4.png)
![$ \mbox{$\displaystyle
\Phi^{(2)}: \underbrace{[0,2] \times [0,2\pi]}_{=:\; K^{...
...) := \begin{pmatrix}r \cos \varphi\\ r \sin \varphi\\ 4-r^2 \end{pmatrix}.
$}$](img5.png)
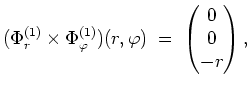
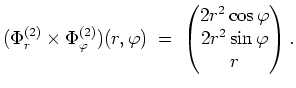
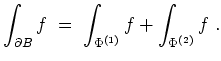
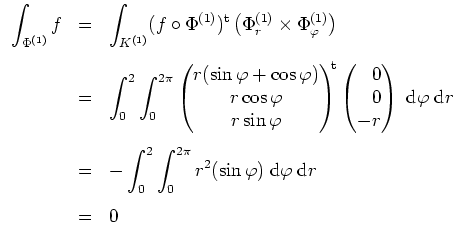
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle \int_{\Phi^{(2)}} f
&=&...
...dfrac{r^4}{4} + 2r^2 \right]_0^2 \vspace{3mm}\\
&=& 24 \pi \; .
\end{array}$}$](img12.png)
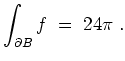
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle \int_{\partial B} f
&=...
...2r^2 - \dfrac{r^4}{4} \right]_0^2\vspace{3mm}\\
&=& 24 \pi \; .
\end{array}$}$](img15.png)