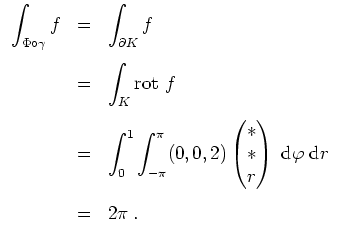Lösung.

Sei $ \mbox{$\Phi: K := [0,1]\times [-\pi,\pi]\longrightarrow\mathbb{R}^3$}$ definiert durch $ \mbox{$\Phi(r,t) = (r\cos t, \, r\sin t, \, r(\cos t)^2)^{\text{t}}$}$ .

Skizze des Trägers von $ \mbox{$\Phi$}$ .

\includegraphics[width = 8cm]{s5.eps}

Den Rand $ \mbox{$\partial K$}$ von $ \mbox{$K$}$ , der sich aus vier Geradenstücken zusammensetzt, beschreiben wir durch die folgenden vier ebenen Kurven.

$ \mbox{$\displaystyle \begin{array}{rcll} \alpha(t) &=& (0,-t)^\text{t}\; , & ... ...mm}\\ \delta(t) &=& (-t,\pi)^\text{t}\; , & t\in [-1,0]\;. \\ \end{array}$}$
Der Rand $ \mbox{$\partial\Phi=\Phi\circ\partial K$}$ der Fläche $ \mbox{$\Phi$}$ wird also beschrieben durch die vier Raumkurven
$ \mbox{$\displaystyle \begin{array}{rcll} (\Phi\circ\alpha)(t) &=& (0,\; 0,\; ... ...hi\circ\delta)(t) &=& (t,\; 0,\;-t)^\text{t}\; , & t\in [-1,0]\;. \end{array}$}$
Eine Betrachtung dieser Wege wird die Rechnung erleichtern. Zunächst ist $ \mbox{$\Phi\circ\alpha$}$ ein konstanter Weg, d.h. ein Kurvenintegral längs dieses Weges ist $ \mbox{$0$}$ . Ferner ist $ \mbox{$\Phi\circ\beta$}$ genau der zu $ \mbox{$\Phi\circ\delta$}$ entgegengesetzte Weg. Die Kurvenintegrale längs dieser beiden Wege heben sich gegenseitig auf. Es bleibt $ \mbox{$\Phi\circ\gamma$}$ zu betrachten.

Weiterhin berechnen wir die Rotation von $ \mbox{$f$}$ zu

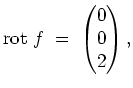
$ \mbox{$\displaystyle \text{rot } f \;=\; \begin{pmatrix}0\\ 0\\ 2\end{pmatrix}, $}$
sowie den Normalenvektor
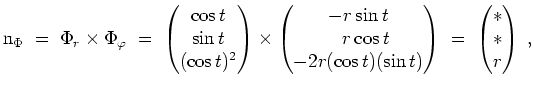
$ \mbox{$\displaystyle \text{n}_\Phi \; =\; \Phi_r\times\Phi_\varphi \; =\; \be... ...)(\sin t) \end{pmatrix} \; =\; \begin{pmatrix}*\\ *\\ r \end{pmatrix}\; , $}$
desssen oberen beiden Einträge uns nicht interessieren.

Der Stokessche Integralsatz liefert unter Beachtung der Tatsache, daß nur $ \mbox{$\Phi\circ\gamma$}$ einen relevanten Beitrag zum Kurvenintegral längs $ \mbox{$\partial K$}$ liefert, also

$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle \int_{\Phi\circ\gamma} ... ...text{d}\varphi \; \text{d}r \vspace{3mm}\\ & = & 2\pi\; .\\ \end{array}$}$