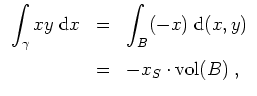
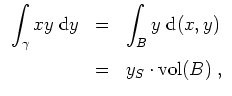
![\includegraphics[width = 8cm]{s3.eps}](img4.png)
Die Kurven
![]() seien definiert durch
seien definiert durch
![$ \mbox{$\displaystyle
\begin{array}{rlcl}
\alpha: [0,2]\to\mathbb{R}^2\;, & \a...
...athbb{R}^2\;, & \delta(t) & = & \displaystyle{t\choose t}\;. \\
\end{array}$}$](img6.png)
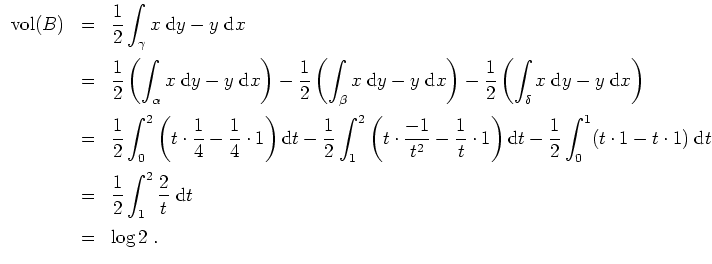
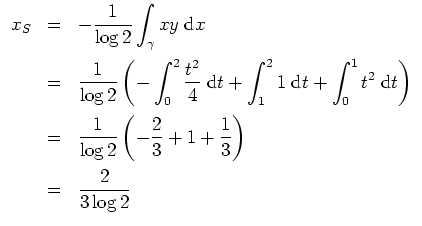
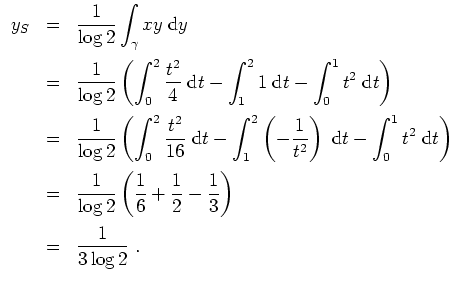
![\includegraphics[width = 8cm]{s3.eps}](img4.png)
Die Kurven
![]() seien definiert durch
seien definiert durch
![$ \mbox{$\displaystyle
\begin{array}{rlcl}
\alpha: [0,2]\to\mathbb{R}^2\;, & \a...
...athbb{R}^2\;, & \delta(t) & = & \displaystyle{t\choose t}\;. \\
\end{array}$}$](img6.png)
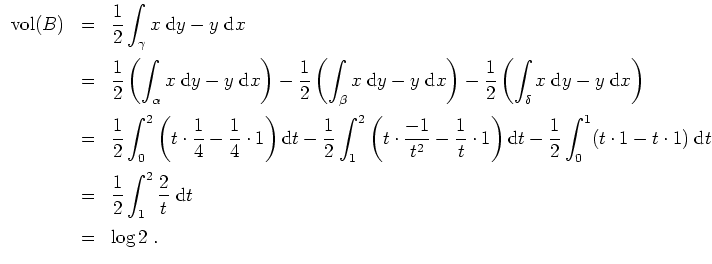
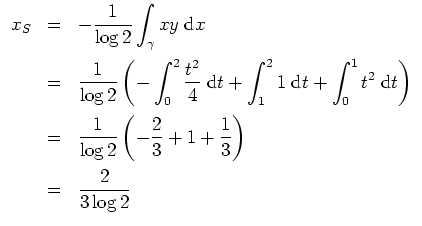
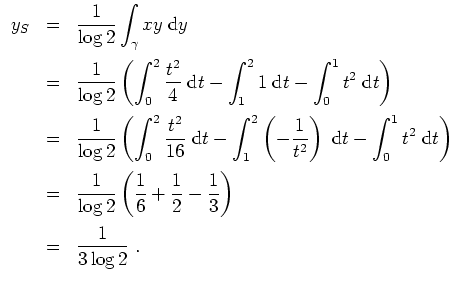
Als Probe prüfe man den resultierenden Schwerpunkt anhand der Skizze auf Plausibilität.
Er sollte in
![]() liegen, und dort auch nicht gerade am Rand.
liegen, und dort auch nicht gerade am Rand.