Wir parametrisieren den Rand
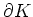 der dreidimensionalen Kugel
der dreidimensionalen Kugel
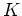 mit Radius
mit Radius
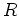 um den Ursprung mittels
um den Ursprung mittels
und bestimmen den Normalenvektor der Fläche
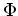 zu
Wir bemerken, daß der Normalenvektor stets nicht nach innen zeigt, und wenden den Gaußschen Integralsatz auf das
Vektorfeld
zu
Wir bemerken, daß der Normalenvektor stets nicht nach innen zeigt, und wenden den Gaußschen Integralsatz auf das
Vektorfeld
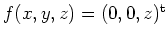 , dessen Divergenz
, dessen Divergenz
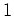 beträgt, an.
beträgt, an.
![]() der dreidimensionalen Kugel
der dreidimensionalen Kugel
![]() mit Radius
mit Radius
![]() um den Ursprung mittels
um den Ursprung mittels
![$ \mbox{$\displaystyle
\Phi:[0,\pi]\times[-\pi,\pi]\to\mathbb{R}^3,\;
\Phi(\ps...
...si)(\cos\varphi)\\ R(\sin\psi)(\sin\varphi)\\ R\cos\psi \end{pmatrix} \, ,
$}$](img4.png)
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\text{vol}(K)
&=& \displaystyle \int...
...^3 \right]_0^\pi\vspace{3mm}\\
&=& \dfrac{4}{3} \; \pi R^3 \, .
\end{array}$}$](img9.png)