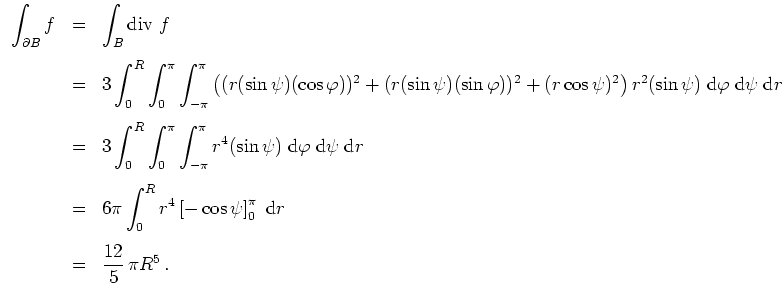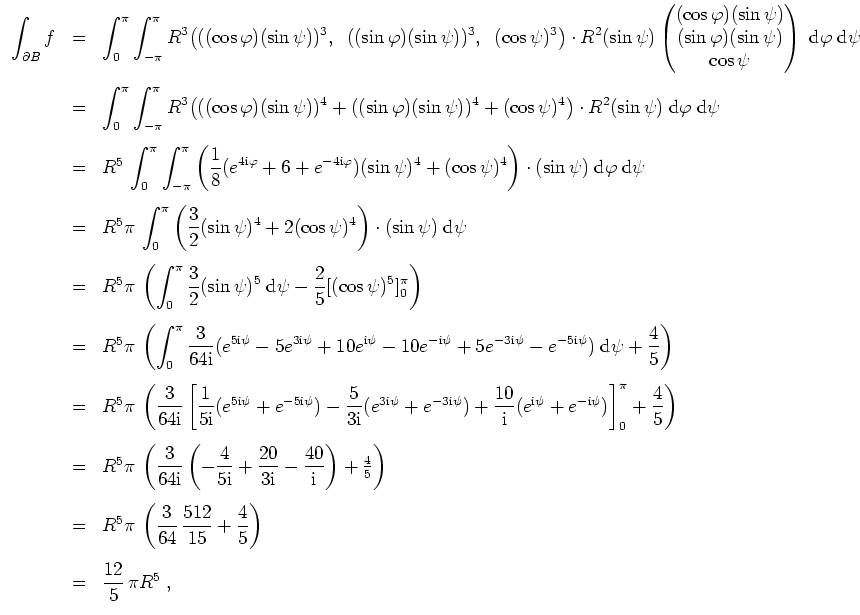Lösung.

Es ist

$ \mbox{$\displaystyle \text{div } f(x,y,z) \; =\; 3 (x^2+y^2+z^2)\; . $}$
Mit dem Gaußschen Integralsatz erhalten wir unter Verwendung von Kugelkoordinaten - bei welchen der Normalenvektor in der Tat stets nicht nach innen zeigt -
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle \int_{\partial B} f &=... ... \; \text{d} r\vspace{3mm}\\ &=& \dfrac{12}{5} \, \pi R^5 \, . \end{array}$}$
Eine direkte Rechnung liefert, ebenfalls unter Verwendung von Kugelkoordinaten, aber etwas mühevoller,
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle \int_{\partial B} f & ... ...5}\right) \vspace{3mm}\\ & = & \dfrac{12}{5} \, \pi R^5\; ,\\ \end{array}$}$
wie zu erwarten.