Lösung.

Wir berechnen das Oberflächenintegral mit dem Stokesschen Integralsatz. Um die Halbkugel zu parametrisieren, wählen wir die Fläche

$ \mbox{$\displaystyle \Phi:\underbrace{[0,\pi/2]\times [-\pi,\pi]}_{=:K} \to\... ...cos \varphi)\\ (\sin \psi)(\sin \varphi)\\ \cos \psi \end{pmatrix}\;. $}$
Den Rand $ \mbox{$\partial K$}$ von $ \mbox{$K$}$ , der sich aus vier Geradenstücken zusammensetzt, beschreiben wir durch die folgenden vier ebenen Kurven.
$ \mbox{$\displaystyle \begin{array}{rcll} \alpha(t) &=& (0,-t)^\text{t}\; , & ... ...ta(t) &=& (-t,\pi)^\text{t}\; , & t\in [-\frac{\pi}{2},0]\;. \\ \end{array}$}$
Der Rand $ \mbox{$\partial\Phi=\Phi\circ\partial K$}$ der Fläche $ \mbox{$\Phi$}$ wird also beschrieben durch die vier Raumkurven
$ \mbox{$\displaystyle \begin{array}{rcll} (\Phi\circ\alpha)(t) &=& (0,\; 0,\; ... ... (\sin t,\; 0,\;\cos t)^\text{t}\; , & t\in [-\frac{\pi}{2},0]\;. \end{array}$}$

Eine Betrachtung dieser Wege wird die Rechnung erleichtern. Zunächst ist $ \mbox{$\Phi\circ\alpha$}$ ein konstanter Weg, d.h. ein Kurvenintegral längs dieses Weges ist $ \mbox{$0$}$ . Ferner ist $ \mbox{$\Phi\circ\beta$}$ genau der zu $ \mbox{$\Phi\circ\delta$}$ entegegengestetzte Weg. Die Kurvenintegrale längs dieser beiden Wege heben sich gegenseitig auf.

Der Stokessche Integralsatz liefert somit

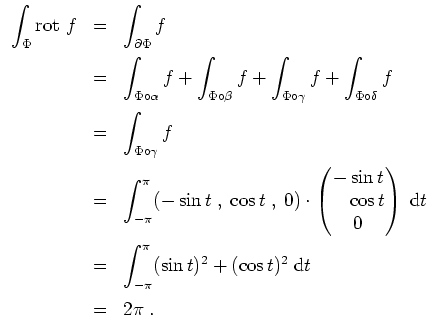
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle\int_\Phi \text{rot }f &... ...\pi (\sin t)^2+(\cos t)^2\;\text{d}t\vspace*{2mm}\\ &=& 2\pi\;. \end{array}$}$

Wollten wir das gegebene Oberflächenintegral direkt berechnen, bestimmen wir noch

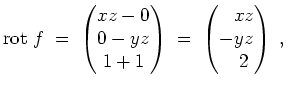
$ \mbox{$\displaystyle \text{rot }f \;=\; \begin{pmatrix}xz-0\\ 0-yz\\ 1+1\en... ...ix}\;=\; \begin{pmatrix}\phantom{-}xz\\ -yz\\ \phantom{-}2\end{pmatrix}\;, $}$
sowie
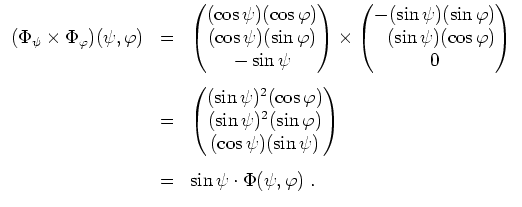
$ \mbox{$\displaystyle \begin{array}{rcl} (\Phi_\psi \times \Phi_\varphi)(\psi,... ...d{pmatrix}\vspace{3mm}\\ &=& \sin\psi\cdot\Phi(\psi,\varphi)\;. \end{array}$}$
Damit ist auch geklärt, daß der Normalenvektor nichtnegative dritte Koordinate hat, d.h. nicht nach unten zeigt. Nach Definition des Oberflächenintegrals ist dann
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle\int_\Phi \text{rot }f &... ...i\left[(\sin\psi)^2\right]_0^{\pi/2}\vspace*{2mm}\\ &=& 2\pi\;. \end{array}$}$
Für das drittletze Gleichheitszeichen beachte man $ \mbox{$\int_{-\pi}^\pi\cos(2\varphi)\;\text{d}\varphi=0$}$ .