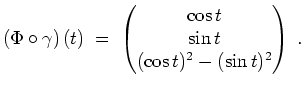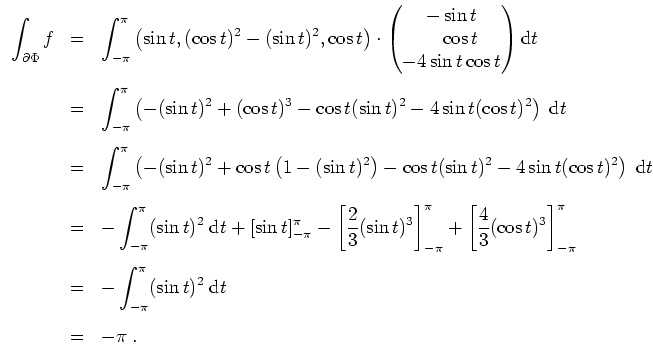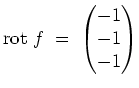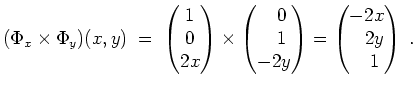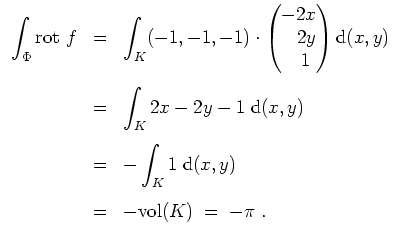Zunächst parametrisieren wir
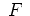 durch
durch
auf
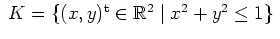 . Dann ist
. Dann ist
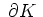 parametrisiert durch die Kurve
Es ist also
parametrisiert durch die Kurve
Es ist also
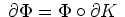 beschrieben durch
Die rechte Seite der Gleichung des Stokesschen Integralsatzes ergibt sich zu
Wir haben
sowie
Die rechte Seite der Gleichung des Stokesschen Integralsatzes ergibt sich zu
Für das drittletzte Gleichheitszeichen beachte man
beschrieben durch
Die rechte Seite der Gleichung des Stokesschen Integralsatzes ergibt sich zu
Wir haben
sowie
Die rechte Seite der Gleichung des Stokesschen Integralsatzes ergibt sich zu
Für das drittletzte Gleichheitszeichen beachte man
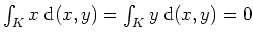 , was sich
aus einer Symmetrieüberlegung ergibt. Diese beiden Integrale berechnen nämlich gerade das
, was sich
aus einer Symmetrieüberlegung ergibt. Diese beiden Integrale berechnen nämlich gerade das
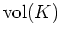 -fache
der Koordinaten des Schwerpunktes von
-fache
der Koordinaten des Schwerpunktes von
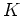 .
.
In der Tat stimmen also die linke und die rechte Seite der Gleichung des Stokesschen Integralsatzes im vorliegenden Fall überein.
![]() durch
durch
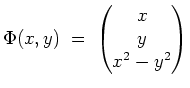
![$ \mbox{$\displaystyle
\gamma(t)\; =\; \begin{pmatrix}\cos t\\ \sin t\end{pmatrix}\;,\quad t\in [-\pi,\pi]\;.
$}$](img5.png)