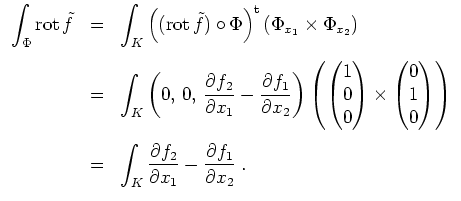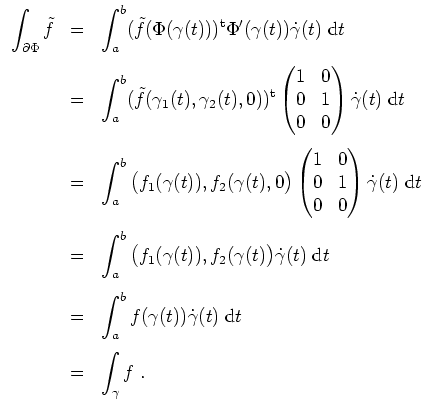Sei
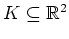 regulär, wobei
regulär, wobei
![$ \mbox{$\gamma:[a,b]\to\mathbb{R}^2$}$](img7.png) den positiv orientierten
Rand
den positiv orientierten
Rand
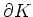 parametrisiere.
Sei
parametrisiere.
Sei
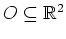 eine offene Obermenge von
eine offene Obermenge von
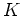 und sei
und sei
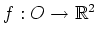 ein stetig
differenzierbares Vektorfeld. Sei
ein stetig
differenzierbares Vektorfeld. Sei
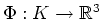 ,
,
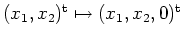 . Dann gilt
. Dann gilt
Sei
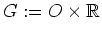 als offene Obermenge von
als offene Obermenge von
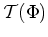 gewählt, und sei
gewählt, und sei
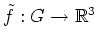 ,
,
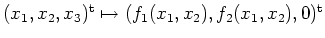 gesetzt.
gesetzt.
Die linke Seite der Gleichung des Stokesschen Integralsatzes für
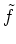 wird zu
wird zu
Die rechte Seite der Gleichung des Stokesschen Integralsatzes für
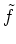 wird zu
Der Stokessche Integralsatz für
wird zu
Der Stokessche Integralsatz für
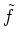 impliziert also den Greenschen Integralsatz für
impliziert also den Greenschen Integralsatz für
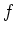 .
.
![]() und
und
![]() .
.
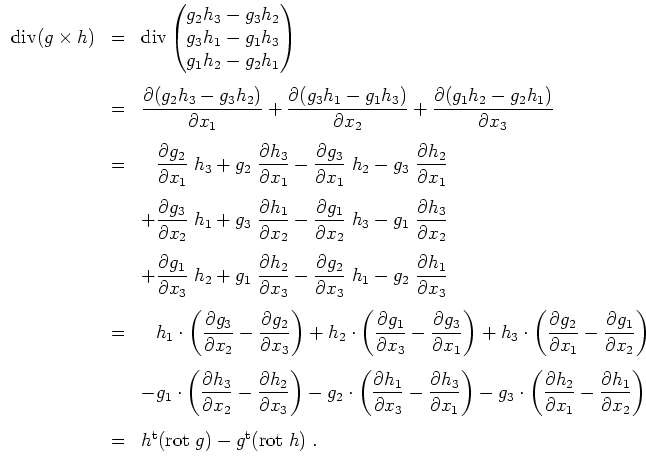
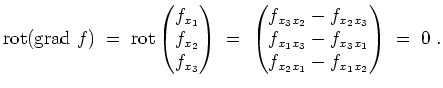
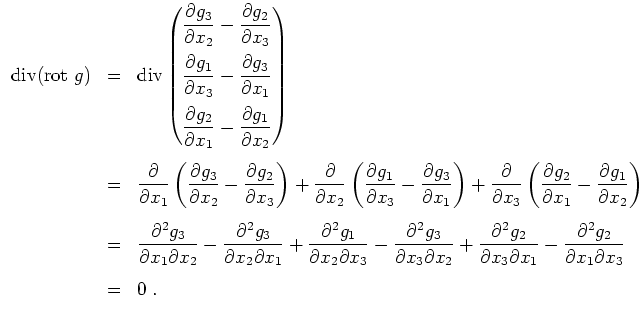
![]() als offene Obermenge von
als offene Obermenge von
![]() gewählt, und sei
gewählt, und sei
![]() ,
,
![]() gesetzt.
gesetzt.
![]() wird zu
wird zu