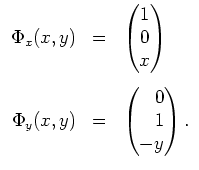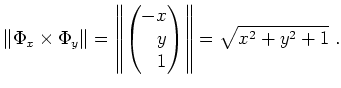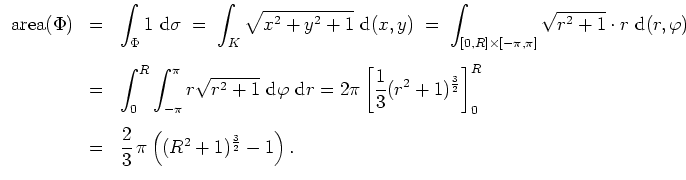Lösung.

(i)

\includegraphics[width=10cm]{torus.eps}

Lösung mit direkter Rechnung.

Wir schreiben

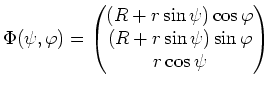
$ \mbox{$\displaystyle \Phi(\psi,\varphi) = \begin{pmatrix}(R+r\sin\psi)\cos\varphi\\ (R+r\sin\psi)\sin\varphi\\ r\cos\psi\end{pmatrix}$}$
mit $ \mbox{$\psi,\varphi\in [0,2\pi]$}$ . Dann sind
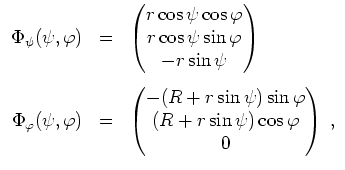
$ \mbox{$\displaystyle \begin{array}{rcl} \Phi_\psi(\psi,\varphi) &=& \begin{pm... ...in\varphi\\ (R+r\sin\psi)\cos\varphi\\ 0\end{pmatrix} \; , \\ \end{array}$}$
und folglich
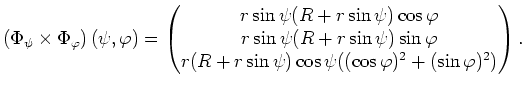
$ \mbox{$\displaystyle \left(\Phi_\psi\times \Phi_\varphi\right)(\psi,\varphi)=... ...phi\\ r(R+r\sin\psi)\cos\psi((\cos\varphi)^2+(\sin\varphi)^2)\end{pmatrix}. $}$
Wir erhalten
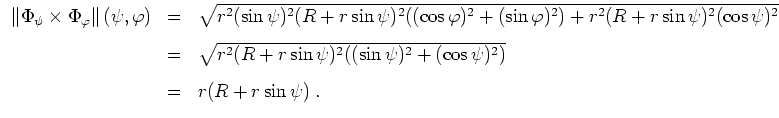
$ \mbox{$\displaystyle \begin{array}{rcl} \left\Vert\Phi_\psi\times \Phi_\varph... ...i)^2+(\cos\psi)^2)}\vspace{3mm}\\ & = & r(R+r\sin\psi) \; .\\ \end{array}$}$
Damit folgt
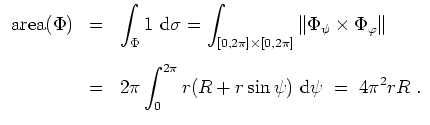
$ \mbox{$\displaystyle \begin{array}{rcl} \text{area}(\Phi) &=& \displaystyle\i... ...\int_0^{2\pi} r(R+r\sin\psi)\ \text{d}\psi \; =\; 4\pi^2 r R \; . \end{array}$}$

Lösung mit der zweiten Guldinschen Regel.

Wir lassen die in der $ \mbox{$x$}$ - $ \mbox{$z$}$ -Ebene liegende Kurve $ \mbox{$\gamma:[0,2\pi] \to \mathbb{R}^2, \, \varphi \mapsto (R + r \cos\varphi, r \sin \varphi)^\text{t}$}$ um die $ \mbox{$z$}$ -Achse rotieren.

Da es sich bei dieser Kurve $ \mbox{$\gamma$}$ um einen Kreis handelt, ist der Kurvenschwerpunkt der Mittelpunkt dieses Kreises, d.h. $ \mbox{$(s_1,s_2)^\text{t} = \left(R,0\right)^\text{t}$}$ .

Die Länge der Kurve beträgt

$ \mbox{$\displaystyle \ell(\gamma) = 2 \pi r \, . $}$
Nach der zweiten Guldinschen Regel ist der Flächeninhalt des so entstehenden Rotationskörpers, d.h. der Flächeninhalt des Torus, gleich
$ \mbox{$\displaystyle \text{area}(\Phi) = \ell(\gamma) \cdot 2\pi s_1 = 4 \pi^2 rR \, . $}$

(ii)

\includegraphics[width=10cm]{paraboloid.eps}

Wir definieren die Fläche

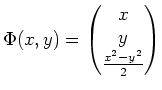
$ \mbox{$\displaystyle \Phi(x,y) = \begin{pmatrix}x\\ y\\ \frac{x^2-y^2}{2}\end{pmatrix}$}$
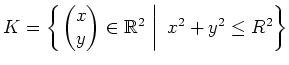auf der kompakten Menge $ \mbox{$K=\left\{\left.\begin{pmatrix}x\\ y\end{pmatrix}\in\mathbb{R}^2\ \right\vert\ x^2+y^2\leq R^2\right\}$}$ . Dann ist $ \mbox{$\Phi(K)=\mathcal P$}$ . Wir berechnen
$ \mbox{$\displaystyle \begin{array}{rcl} \Phi_x(x,y) &=& \begin{pmatrix}1\\ 0... ...(x,y) &=& \begin{pmatrix}\hfill 0\\ \hfill 1\\ -y\end{pmatrix}. \end{array}$}$
Somit ist
$ \mbox{$\displaystyle \Vert\Phi_x\times\Phi_y\Vert=\left\Vert\begin{pmatrix}-x\\ \hfill y\\ \hfill 1\end{pmatrix}\right\Vert=\sqrt{x^2+y^2+1}\; . $}$
Wir erhalten mit der Polarkoordinatentransformation
$ \mbox{$\displaystyle \begin{array}{rcl} \text{area}(\Phi) &=& \displaystyle\i... ...m}\\ &=& \dfrac{2}{3}\,\pi\left((R^2+1)^{\frac{3}{2}}-1\right). \end{array}$}$