Flächen und Oberflächenintegrale.

Sei $ \mbox{$K\subseteq\mathbb{R}^2$}$ eine kompakte meßbare Menge.

Eine Fläche (im dreidimensionalen Raum) ist eine Funktion $ \mbox{$\Phi:K\to\mathbb{R}^3$}$ derart, daß es eine offene Obermenge $ \mbox{$O\supseteq K$}$ gibt und sich $ \mbox{$\Phi$}$ fortsetzen läßt zu einer stetig differenzierbaren Funktion $ \mbox{$\tilde{\Phi}:O\to\mathbb{R}^3$}$ .

Der Grund für die Forderung der Existenz der größeren Menge $ \mbox{$O$}$ und der Fortsetzung $ \mbox{$\tilde{\Phi}$}$ ist, daß wir auch in Randpunkten von $ \mbox{$K$}$ die Ableitung von $ \mbox{$\Phi$}$ betrachten wollen. Kurz gesagt, ist $ \mbox{$\Phi:K\to\mathbb{R}^3$}$ eine ,,auch auf dem Rand von $ \mbox{$K\;$}$ `` stetig differenzierbare Funktion.

Die Bildmenge $ \mbox{$\mathcal{T}(\Phi):=\Phi(K)\subseteq\mathbb{R}^3$}$ heißt der Träger von $ \mbox{$\Phi$}$ .

Der Normalenvektor $ \mbox{$\text{n}_\Phi$}$ der Fläche $ \mbox{$\Phi$}$ ist an jedem Punkt $ \mbox{$(x_1,x_2)^\text{t}\in K$}$ definiert durch

$ \mbox{$\displaystyle \text{n}_{\Phi}(x_1,x_2)\;:=\; \Phi_{x_1}(x_1,x_2)\times\Phi_{x_2}(x_1,x_2)\;. $}$

Wir erinnnern dabei an die Definition des Kreuzproduktes

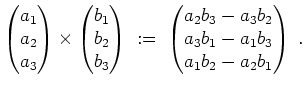
$ \mbox{$\displaystyle \begin{pmatrix}a_1\\ a_2\\ a_3\end{pmatrix}\times\begi... ...egin{pmatrix}a_2b_3-a_3b_2\\ a_3b_1-a_1b_3\\ a_1b_2-a_2b_1\end{pmatrix}\;. $}$
Das Kreuzprodukt zweier Vektoren ist ein Vektor, der zu beiden Faktoren orthogonal ist, und dessen Länge dem Flächeninhalt des von den beiden Faktoren aufgespannten Parallelogramm entspricht. $ \mbox{$\Phi_{x_1}(x)$}$ und $ \mbox{$\Phi_{x_2}(x)$}$ sind zwei Tangentialvektoren in $ \mbox{$\Phi(x)$}$ an $ \mbox{$\mathcal{T}(\Phi)$}$ .

Oberflächenintegral eines Vektorfeldes.

Es sei $ \mbox{$f:\mathcal{T}(\Phi)\to\mathbb{R}^3$}$ ein stetiges Vektorfeld. Dann definieren wir das Oberflächenintegral von $ \mbox{$f$}$ über $ \mbox{$\Phi$}$ vermöge

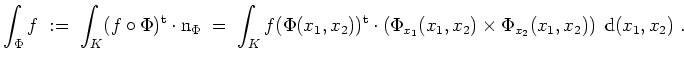
$ \mbox{$\displaystyle \int_\Phi f \;:=\; \int_K (f\circ\Phi)^\text{t}\cdot\tex... ...(\Phi_{x_1}(x_1,x_2) \times\Phi_{x_2}(x_1,x_2)\right)\;\text{d}(x_1,x_2)\;. $}$

Oberflächenintegral einer skalaren Funktion.

Es sei $ \mbox{$g:\mathcal{T}(\Phi)\to\mathbb{R}$}$ eine stetige skalare Funktion. Dann definieren wir das Oberflächenintegral von $ \mbox{$g$}$ über $ \mbox{$\Phi$}$ vermöge

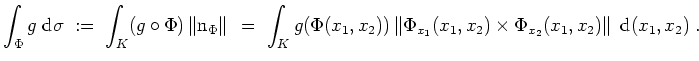
$ \mbox{$\displaystyle \displaystyle\int_\Phi g\;\text{d}\sigma \;:=\; \displa... ...i_{x_1}(x_1,x_2) \times\Phi_{x_2}(x_1,x_2)\right\Vert\;\text{d}(x_1,x_2)\;. $}$

Das Integrationselement $ \mbox{$\text{d}\sigma$}$ steht dabei für die Integration über eine Fläche, englisch ,,surface``.

So ist z.B. der Flächeninhalt der Fläche $ \mbox{$\Phi$}$ definiert als

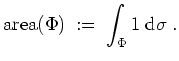
$ \mbox{$\displaystyle \text{area}(\Phi) \;:=\; \int_\Phi 1\;\text{d}\sigma\;. $}$

Das Oberflächenintegral ist in gewissem Sinne nur abhängig vom Träger $ \mbox{$\mathcal{T}(\Phi)$}$ und von der Orientierung der Fläche. Genauer, ist $ \mbox{$\tilde{K}\subseteq\mathbb{R}^2$}$ eine weitere kompakte meßbare Menge, $ \mbox{$\tilde{\Phi}:\tilde{K}\to\mathbb{R}^3$}$ eine stetig differenzierbare Funktion, und ist $ \mbox{$\psi:K\to\tilde{K}$}$ eine stetig differenzierbare bijektive Abbildung so, daß $ \mbox{$\Phi=\tilde{\Phi}\circ\psi$}$ und $ \mbox{$\det\psi\,'>0$}$ überall, so heißen die Flächen $ \mbox{$\Phi$}$ und $ \mbox{$\tilde{\Phi}$}$ äquivalent. Es gelten dann

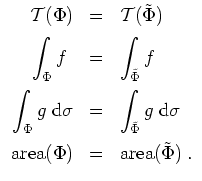
$ \mbox{$\displaystyle \begin{array}{rcl} \mathcal{T}(\Phi) &=& \mathcal{T}(\ti... ...pace*{2mm}\\ \text{area}(\Phi) &=& \text{area}(\tilde{\Phi})\;. \end{array}$}$

Der Kurvenschwerpunkt und die 2. Guldinsche Regel.

Sei $ \mbox{$\gamma=(\gamma_1,\ldots,\gamma_n)^\text{t}:[a,b]\to\mathbb{R}^n$}$ ein Weg mit $ \mbox{$\ell(\gamma)>0$}$ . Dann heißt der Punkt $ \mbox{$(s_1,\ldots,s_n)^\text{t}\in\mathbb{R}^n$}$ mit den Koordinaten

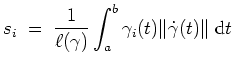
$ \mbox{$\displaystyle s_i \;=\; \dfrac{1}{\ell(\gamma)}\int_a^b \gamma_i(t)\Vert\dot{\gamma}(t)\Vert\;\text{d}t $}$
der Kurvenschwerpunkt von $ \mbox{$\gamma$}$ .

Sei nun speziell $ \mbox{$\gamma=(\gamma_1,\gamma_2)^\text{t}:[a,b]\to\mathbb{R}_{\geq 0}\times\mathbb{R}$}$ ein Weg mit Kurvenschwerpunkt $ \mbox{$(s_1,s_2)^\text{t}$}$ . Sei $ \mbox{$\Phi$}$ die aus $ \mbox{$\gamma$}$ entstehende Rotationsfläche bei Drehung um die $ \mbox{$y$}$ -Achse, d.h. $ \mbox{$\Phi$}$ ist die Fläche mit der Parametrisierung

$ \mbox{$\displaystyle \Phi:[a,b]\times[0,2\pi]\to\mathbb{R}^3\;,\;\; \Phi(t,\v... ...amma_1(t)\cos\varphi\;,\;\gamma_2(t)\;,\;\gamma_1(t)\sin\varphi)^\text{t}\;. $}$
Der 2. Guldinschen Regel zufolge berechnet sich nun den Flächeninhalt von $ \mbox{$\Phi$}$ zu
$ \mbox{$\displaystyle \text{area}(\Phi) \;=\; \ell(\gamma)\cdot 2\pi s_1\;. $}$
Mit anderen Worten, der Flächeninhalt der Rotationsfläche $ \mbox{$\Phi$}$ ist gleich der Länge des Weges $ \mbox{$\gamma$}$ , multipliziert mit der Länge des bei der Rotation zurückgelegten Weges des Kurvenschwerpunktes.