Lösung.

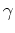Sei $ \mbox{$\gamma$}$ die Kurve, die den Graphen von 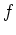$ \mbox{$f$}$ beschreibt, d.h. sei

$ \mbox{$\displaystyle \gamma:[a,b]\to\mathbb{R}^2\; ,\;\;\; \gamma(t)\; :=\; {t\choose f(t)}\;. $}$
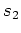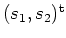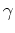  1. Die zweite Koordinate $ \mbox{$s_2$}$ des Kurvenschwerpunkts $ \mbox{$(s_1,s_2)^\text{t}$}$ von $ \mbox{$\gamma$}$ ist gegeben durch
    $ \mbox{$\displaystyle s_2 \;=\; \dfrac{1}{\ell(\gamma)}\int_a^b\gamma_2(t)\Ve... ...t \;=\; \dfrac{1}{\ell(\gamma)}\int_a^b f(t)\sqrt{1+(f'(t))^2}\;\text{d}t\;. $}$
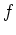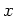    Also ergibt sich der gesuchte Flächeninhalt der Rotationsfläche des Graphen von $ \mbox{$f$}$ um die $ \mbox{$x$}$ -Achse mit der zweiten Guldinschen Regel zu
    $ \mbox{$\displaystyle \text{area}(\Phi) \;=\; \ell(\gamma)\cdot 2\pi s_2 \;=\; 2\pi\int_a^b f(t)\sqrt{1+(f'(t))^2}\;\text{d}t\;. $}$

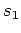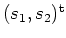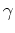  2. Die erste Koordinate $ \mbox{$s_1$}$ des Kurvenschwerpunkts $ \mbox{$(s_1,s_2)^\text{t}$}$ von $ \mbox{$\gamma$}$ ist gegeben durch
    $ \mbox{$\displaystyle s_1 \;=\; \dfrac{1}{\ell(\gamma)}\int_a^b\gamma_1(t)\Ve... ...{d}t \;=\; \dfrac{1}{\ell(\gamma)}\int_a^b t\sqrt{1+(f'(t))^2}\;\text{d}t\;. $}$
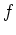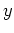    Also ergibt sich der gesuchte Flächeninhalt der Rotationsfläche des Graphen von $ \mbox{$f$}$ um die $ \mbox{$y$}$ -Achse mit der zweiten Guldinschen Regel zu
    $ \mbox{$\displaystyle \text{area}(\Phi) \;=\; \ell(\gamma)\cdot 2\pi s_1 \;=\; 2\pi\int_a^b t\sqrt{1+(f'(t))^2}\;\text{d}t\;. $}$

  3. Sei $ \mbox{$f:[0,h]\to\mathbb{R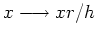}$}$ , $ \mbox{$x\longrightarrow xr/h$}$ . Die zugehörige Rotationsfläche um die 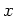$ \mbox{$x$}$ -Achse ist die gesuchte Mantelfläche und ergibt sich mit 1. zu
    $ \mbox{$\displaystyle \begin{array}{rcl} 2\pi\displaystyle\int_0^h f(t)\sqrt{1... ...c{h^2}{2} \vspace*{2mm} \\ & = & \pi r\sqrt{r^2 + h^2}\; . \\ \end{array}$}$

  4. Sei $ \mbox{$f:[-r,+r]\to\mathbb{R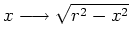}$}$ , $ \mbox{$x\longrightarrow \sqrt{r^2 - x^2}$}$ . Die zugehörige Rotationsfläche um die 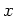$ \mbox{$x$}$ -Achse ist die gesuchte Kugeloberfläche und ergibt sich mit 1. zu
    $ \mbox{$\displaystyle \begin{array}{rcl} 2\pi\displaystyle\int_{-r}^r f(t)\sqr... ...ext{d}t \vspace*{2mm} \\ & = & 4\pi r^2 \; . \vspace*{2mm} \\ \end{array}$}$

  5. Sei $ \mbox{$f:[-1,+1]\to\mathbb{R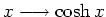}$}$ , $ \mbox{$x\longrightarrow \cosh x$}$ . Die zugehörige Rotationsfläche um die $ \mbox{$x$}$ -Achse ergibt sich mit 1. zu
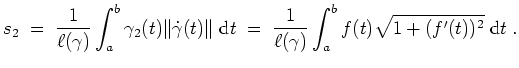
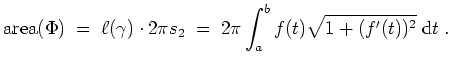
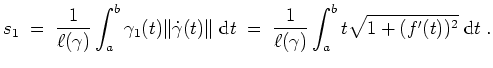
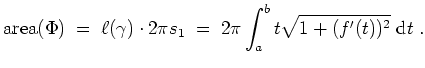
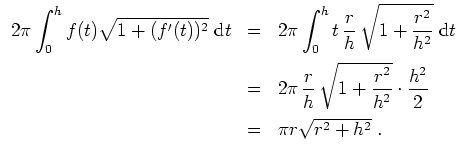
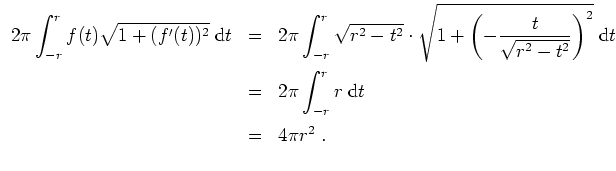
    $ \mbox{$\displaystyle \begin{array}{rcl} 2\pi\displaystyle\int_{-1}^1 f(t)\sqr... ...}\right]_{-1}^1\vspace*{2mm} \\ & = & \pi(2 + \sinh 2)\; . \\ \end{array}$}$