Lösung.

Wir berechnen zunächst den Normalenvektor der Fläche $ \mbox{$\Phi$}$ durch

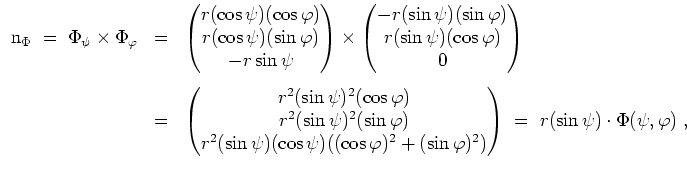
$ \mbox{$\displaystyle \begin{array}{rcl} \text{n}_{\Phi} \;=\; \Phi_\psi\times... ...arphi)^2)\end{pmatrix}\;=\; r(\sin\psi)\cdot\Phi(\psi,\varphi)\;, \end{array}$}$
was der Anschauuung entspricht, daß der Vektor vom Ursprung zu einem Punkt auf der Kugel normal zur Kugeloberfläche steht.

Also errechnet sich der Flächeninhalt der Kugel unter Beachtung von $ \mbox{$\Vert\Phi(\psi,\varphi)\Vert=r$}$ zu

$ \mbox{$\displaystyle \begin{array}{rcl} \text{area}(\Phi) &=& \displaystyle\i... ...r^2 \left[-\cos\psi\right]_0^\pi\vspace*{4mm}\\ &=& 4\pi r^2\;. \end{array}$}$

Der Flächeninhalt des Kreises mit Radius $ \mbox{$r$}$ ist $ \mbox{$\pi r^2$}$ , ihr Umfang ist davon die Ableitung nach $ \mbox{$r$}$ , nämlich $ \mbox{$2\pi r$}$ .

Das Volumen der Kugel mit Radius $ \mbox{$r$}$ ist $ \mbox{$4\pi r^3/3$}$ , ihre Oberfläche ist, wie eben gesehen, davon die Ableitung nach $ \mbox{$r$}$ , nämlich $ \mbox{$4\pi r^2$}$ .

Warum?