Lösung.

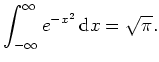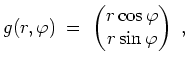
Verwenden wir die Polarkoordinatentransformation

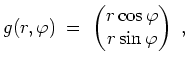
$ \mbox{$\displaystyle g(r,\varphi) \; =\; \begin{pmatrix}r \cos \varphi\\ r \sin \varphi \end{pmatrix} \; , $}$
so ist $ \mbox{$K_\rho = g(M_\rho)$}$ mit
$ \mbox{$\displaystyle M_\rho \; :=\; \{ (r, \varphi)^\text{t} \in \mathbb{R}^2 \; \vert\; 0 \leq r \leq \rho, 0 \leq \varphi \leq \pi/2 \} \; . $}$
Mittels der Substitutionsregel errechnen wir
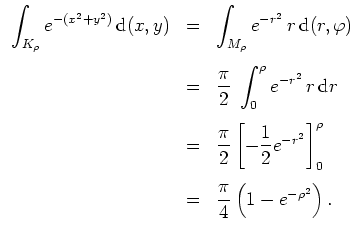
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle \int_{K_\rho} e^{-(x^2... ...e{3mm}\\ & = & \dfrac{\pi}{4} \left( 1 - e^{- \rho^2} \right). \end{array}$}$

Der Satz von Fubini liefert

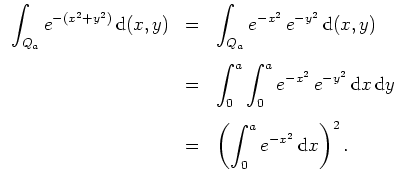
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle \int_{Q_a} e^{-(x^2 + ... ... & \displaystyle \left( \int_0^a e^{-x^2} \, \text{d}x \right)^2. \end{array}$}$

Es ist

$ \mbox{$\displaystyle K_a \subseteq Q_a \subseteq K_{\sqrt{2} a} $}$
für alle $ \mbox{$a \geq 0$}$ . Skizze für $ \mbox{$a = 1$}$ :
\includegraphics[width = 4cm]{s3.eps}

Da wir über eine nichtnegative Funktion integrieren, erhalten wir den Zusammenhang

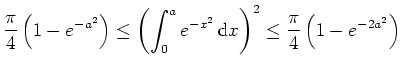
$ \mbox{$\displaystyle \displaystyle \dfrac{\pi}{4} \left( 1 - e^{- a^2} \righ... ...} \, \text{d}x \right)^2 \leq \dfrac{\pi}{4} \left( 1 - e^{- 2 a^2} \right) $}$
für alle $ \mbox{$a \geq 0$}$ . Im Grenzübergang $ \mbox{$a$}$ gegen $ \mbox{$\infty$}$ erhalten wir hieraus
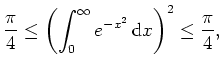
$ \mbox{$\displaystyle \displaystyle \dfrac{\pi}{4} \leq \left( \int_0^\infty e^{-x^2} \, \text{d}x \right)^2 \leq \dfrac{\pi}{4}, $}$
d.h.
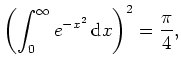
$ \mbox{$\displaystyle \displaystyle \left( \int_0^\infty e^{-x^2} \, \text{d}x \right)^2 = \dfrac{\pi}{4}, $}$
und somit
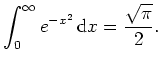
$ \mbox{$\displaystyle \displaystyle \int_0^\infty e^{-x^2} \, \text{d}x = \dfrac{\sqrt{\pi}}{2}. $}$

Nutzen wir nun die Symmetrie der Funktion $ \mbox{$f:\mathbb{R}\to\mathbb{R}, \, x \mapsto e^{-x^2}$}$ bezüglich der $ \mbox{$y$}$ -Achse aus, so erhalten wir die Behauptung,

$ \mbox{$\displaystyle \displaystyle \int_{-\infty}^\infty e^{-x^2} \, \text{d}x = \sqrt{\pi}. $}$