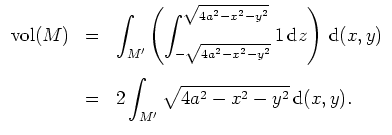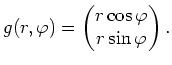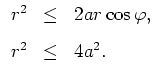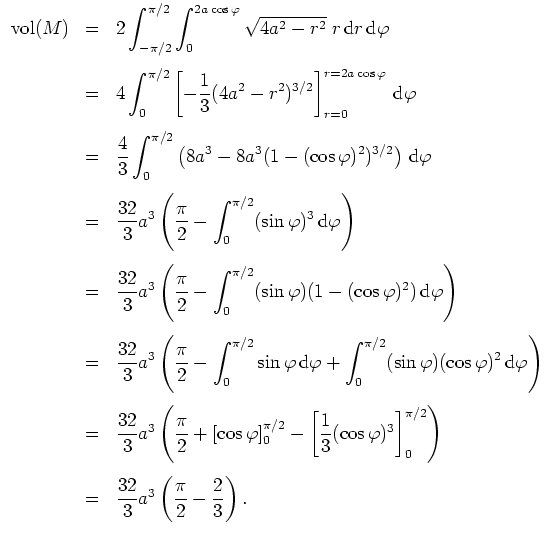Es sei
Mit dem Satz von Fubini erhalten wir somit zunächst
Wir betrachten nun die Polarkoordinatentransformation
Wir erhalten damit als Integrationsbereich
Es sei zunächst
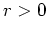 . Lösen wir die beiden obigen Ungleichungen nach
. Lösen wir die beiden obigen Ungleichungen nach
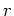 auf, so sehen wir, daß die zweite
Ungleichung stets erfüllt ist, sofern nur die erste gilt. Nun bemerken wir, daß diese Beobachtung trivialerweise auch
für
auf, so sehen wir, daß die zweite
Ungleichung stets erfüllt ist, sofern nur die erste gilt. Nun bemerken wir, daß diese Beobachtung trivialerweise auch
für
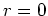 zutrifft. Wir können die zweite Ungleichung also in unseren weiteren Betrachtungen vernachlässigen und
erhalten mit der Achsensymmetrie des Cosinus
zutrifft. Wir können die zweite Ungleichung also in unseren weiteren Betrachtungen vernachlässigen und
erhalten mit der Achsensymmetrie des Cosinus