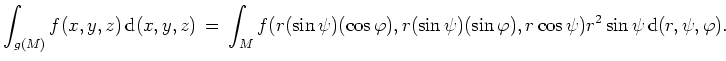Sei folgende Situation gegeben.
Wir wollen die Funktion
![]() integrieren, und dazu
integrieren, und dazu
![]() substituieren. Die genannten Bedingungen an
substituieren. Die genannten Bedingungen an
![]() besagen hierbei grob gesprochen, daß
besagen hierbei grob gesprochen, daß
![]() hierzu überall regulär sein soll, ausgenommen möglicherweise auf einer vernachlässigbaren Teilmenge
hierzu überall regulär sein soll, ausgenommen möglicherweise auf einer vernachlässigbaren Teilmenge
![]() .
.
Es gilt die Substitutionsregel
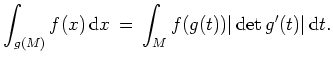
Wir führen drei wichtige Anwendungen der mehrdimensionalen Substitutionsregel auf.
Polarkoordinaten im
![]() .
.
Die Polarkoordinaten
![]() eines Punktes
eines Punktes
![]() sind definiert durch die Gleichungen
sind definiert durch die Gleichungen
![]() und
und
![]() .
.
Betrachtet man die Polarkoordinatentransformation
![]() ,
,
![]() , so ist
, so ist
![]() stetig differenzierbar mit
stetig differenzierbar mit
![]() .
.
Seien
![]() kompakt,
kompakt,
![]() meßbar und
meßbar und
![]() stetig.
stetig.
Dann gilt
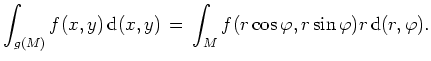
Wir bemerken, daß in der Anwendung in der Regel zunächst
![]() gegeben ist, und man sich dazu
gegeben ist, und man sich dazu
![]() geeignet suchen muß.
geeignet suchen muß.
Zylinderkoordinaten im
![]() .
.
Die Zylinderkoordinaten
![]() eines Punktes
eines Punktes
![]() sind definiert durch die Gleichungen
sind definiert durch die Gleichungen
![]() ,
,
![]() und
und
![]() .
.
Betrachtet man die Zylinderkoordinatentransformation
![]() ,
,
![]() , so ist
, so ist
![]() stetig differenzierbar mit
stetig differenzierbar mit
![]() .
.
Seien
![]() kompakt,
kompakt,
![]() meßbar und
meßbar und
![]() stetig.
stetig.
Dann gilt
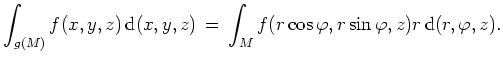
Kugelkoordinaten im
![]() .
.
Die Kugelkoordinaten
![]() eines Punktes
eines Punktes
![]() sind definiert durch die Gleichungen
sind definiert durch die Gleichungen
![]() ,
,
![]() und
und
![]() .
.
Betrachtet man die Kugelkoordinatentransformation
![]() ,
,
![]() , so ist
, so ist
![]() stetig differenzierbar mit
stetig differenzierbar mit
![]() .
.
Seien
![]() kompakt,
kompakt,
![]() meßbar und
meßbar und
![]() stetig.
stetig.
Dann gilt