Lösung.

Zunächst betrachten wir den Schnitt $ \mbox{$M^y=\{x\in\mathbb{R}\ \vert\ (x,y)^\text{t}\in M\}$}$ . Diese Menge ist leer, falls $ \mbox{$\vert y\vert>r$}$ ist. Für $ \mbox{$\vert y\vert\leq r$}$ erhalten wir die Bedingungen

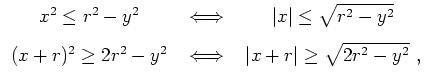
$ \mbox{$\displaystyle \begin{array}{ccc} x^2\leq r^2-y^2&\iff&\vert x\vert\leq... ... (x+r)^2\geq 2r^2-y^2&\iff&\vert x+r\vert\geq\sqrt{2r^2-y^2}\ , \end{array}$}$
also
$ \mbox{$\displaystyle -r+\sqrt{2r^2-y^2}\;\le\; x\;\le\; \sqrt{r^2-y^2}\; , $}$
und somit
$ \mbox{$\displaystyle M^y\; =\; \begin{cases} \emptyset & \text{f\uml ur {$\m... ...2-y^2}] & \text{f\uml ur {$\mbox{$\vert y\vert\leq r$}$}}\; .\\ \end{cases}$}$
Also ist
$ \mbox{$\displaystyle M'\; =\;\{y\in\mathbb{R}\; \vert\; M^y\neq\emptyset\} \; =\; [-r,r]\; . $}$
Wir berechnen
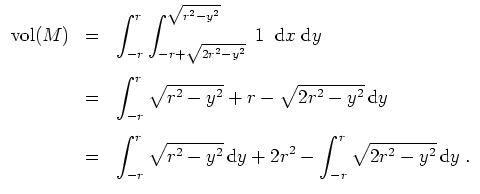
$ \mbox{$\displaystyle \begin{array}{rcl} \text{vol}(M) & = & \displaystyle\int... ...ext{d}y + 2r^2 - \int_{-r}^r \sqrt{2r^2-y^2}\,\text{d}y \; . \\ \end{array}$}$
Eine Nebenrechnung mit partieller Integration gibt
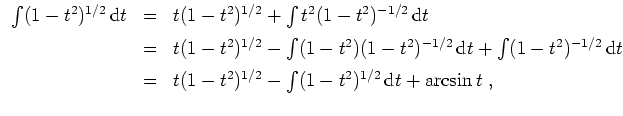
$ \mbox{$\displaystyle \begin{array}{rcl} \int (1-t^2)^{1/2}\,\text{d} t & = & ... ...- \int (1-t^2)^{1/2}\,\text{d} t + \arcsin t\; , \vspace{2mm}\\ \end{array}$}$
und somit
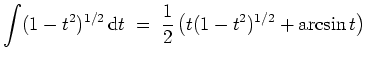
$ \mbox{$\displaystyle \int (1-t^2)^{1/2}\,\text{d} t \;=\; \frac{1}{2}\left( t(1-t^2)^{1/2} + \arcsin t\right) $}$
Wir können fortfahren mit
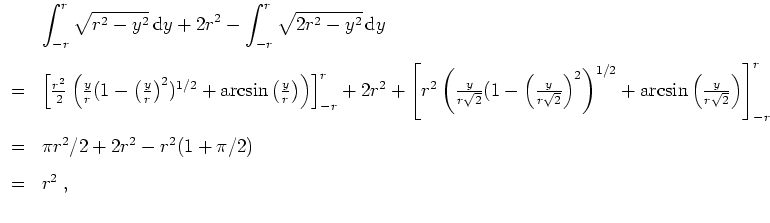
$ \mbox{$\displaystyle \begin{array}{cl} & \displaystyle\int_{-r}^r \sqrt{r^2-... ... - r^2(1 + \pi/2) \vspace{3mm} \\ = & r^2\; , \vspace{3mm} \\ \end{array}$}$
d.h. $ \mbox{$\text{vol}(M) = r^2$}$ .

Es ist eine gute Probe, das Ergebnis mit der Anschauung zu vergleichen, vgl. Aufgabenstellung.

Außerdem, wenn eine Figur in $ \mbox{$\mathbb{R}^n$}$ von einem Parameter $ \mbox{$r$}$ zentral gestreckt wird, wie etwa im vorliegenden Fall, so ist ihr Inhalt proportional zu $ \mbox{$r^n$}$ .