Das mehrdimensionale Riemann-Integral.

Integration über Quader.

Es seien $ \mbox{$n\ge 1$}$ und $ \mbox{$a_1,\ldots,a_n, b_1,\ldots,b_n \in \mathbb{R}$}$ mit $ \mbox{$a_i < b_i$}$ für alle $ \mbox{$i\in\{1,\ldots,n\}$}$ . Es ist $ \mbox{$I := [a_1, b_1] \times \ldots \times [a_n, b_n]\subseteq\mathbb{R}^n$}$ ein n-dimensionaler Quader. Dessen Volumen ist definiert als

$ \mbox{$\displaystyle \text{vol}(I) \; :=\; (b_1 - a_1)(b_2 - a_2) \cdots (b_n - a_n)\; . $}$

Sei für alle $ \mbox{$i\in\{1,\ldots,n\}$}$ eine Unterteilung $ \mbox{$\underline{x}^{(i)} = (a_i = x_0^{(i)} < x_1^{(i)} < x_2^{(i)} < \cdots < x_{k_i}^{(i)} = b_i)$}$ von $ \mbox{$[a_i,b_i]$}$ gewählt. Dann heißt das kartesische Produkt

$ \mbox{$\displaystyle \underline{x} \; = \; \underline{x}^{(1)} \times \dots \times \underline{x}^{(n)} $}$
eine Unterteilung des Quaders $ \mbox{$I$}$ .

Zum Beispiel ist $ \mbox{$(0 < 1 < 2)\times (3 < 6) = \{ (0,3),\, (0,6),\, (1,3),\, (1,6),\, (2,3),\, (2,6)\}$}$ eine Unterteilung des Quaders $ \mbox{$[0,2]\times [3,6]$}$ .

Für jedes Tupel $ \mbox{$\underline{\nu}=(\nu_1, \ldots, \nu_n)$}$ mit $ \mbox{$1 \leq \nu_i \leq k_i$}$ für $ \mbox{$i\in\{1,\ldots,n\}$}$ heißt

$ \mbox{$\displaystyle I_{\underline{x},\underline{\nu}} \; :=\; \left[x_{\nu_... ...right] \times \dots \times \left[x_{\nu_n-1}^{(n)}, x_{\nu_n}^{(n)}\right] $}$
ein Teilquader von $ \mbox{$I$}$ zur Unterteilung $ \mbox{$\underline{x}$}$ .

Sei $ \mbox{$f:I\to\mathbb{R}$}$ eine beschränkte Funktion.

Das Volumen zwischen der $ \mbox{$x_1, \ldots, x_n$}$ -Ebene und dem Funktionsgraphen wird von oben angenähert durch die Obersumme

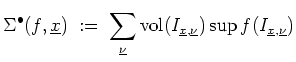
$ \mbox{$\displaystyle \Sigma^\bullet(f,\underline{x}) \; :=\; \sum_{\underline... ...I_{\underline{x},\underline{\nu}}) \sup f(I_{\underline{x},\underline{\nu}}) $}$
und von unten durch die Untersumme
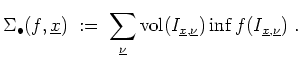
$ \mbox{$\displaystyle \Sigma_\bullet(f,\underline{x}) \; :=\; \sum_{\underline... ...nderline{x},\underline{\nu}}) \inf f(I_{\underline{x},\underline{\nu}}) \; . $}$
Dabei erstrecken sich die Summen über alle möglichen Tupel $ \mbox{$\underline{\nu}$}$ wie oben beschrieben. Stimmen das Supremum der Untersummen und das Infimum der Obersummen, genommen über alle Unterteilungen von $ \mbox{$I$}$ , überein, so heißt $ \mbox{$f$}$ (Riemann-) integrierbar auf $ \mbox{$I$}$ , und wir schreiben
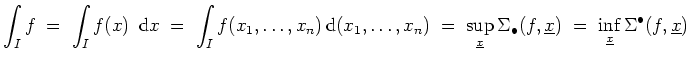
$ \mbox{$\displaystyle \int_I f \; =\; \int_I f(x) \,\text{d}x\; = \; \int_I f(... ...t(f,\underline{x})\; =\; \inf_{\underline{x}}\Sigma^\bullet(f,\underline{x}) $}$
für das Integral von $ \mbox{$f$}$ über $ \mbox{$I$}$ .

Anschaulich beziffert das Integral also das Volumen zwischen der $ \mbox{$x_1, \ldots, x_n$}$ -Ebene und dem Funktionsgraphen, wobei die Teile unterhalb der $ \mbox{$x_1, \ldots, x_n$}$ -Ebene negativ zu nehmen sind.

Iterierte Integrale und der Satz von Fubini für Quader.

Für fest gewähltes $ \mbox{$m \in \{1, \ldots, n-1\}$}$ betrachte die Quader $ \mbox{$I', I''$}$ mit

$ \mbox{$\displaystyle I \; =\; \underbrace{[a_1,b_1] \times \ldots \times [a_... ...\underbrace{[a_{m+1},b_{m+1}] \times \ldots \times [a_n,b_n]}_{=:\; I''}\; . $}$
Der Satz von Fubini für Quader besagt nun, daß einerseits
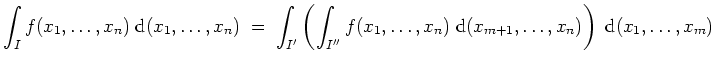
$ \mbox{$\displaystyle \int_I f(x_1, \ldots, x_n) \; \text{d}(x_1, \ldots, x_n... ..._n) \; \text{d}(x_{m+1}, \ldots, x_n)\right) \; \text{d}(x_1, \ldots, x_m) $}$
gilt, falls alle auftretenden Integrale existieren, und daß andererseits
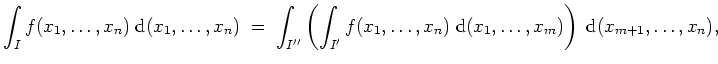
$ \mbox{$\displaystyle \int_I f(x_1, \ldots, x_n) \; \text{d}(x_1, \ldots, x_n... ... \; \text{d}(x_{1}, \ldots, x_m)\right) \; \text{d}(x_{m+1}, \ldots, x_n), $}$
falls wiederum alle auftretenden Integrale existieren. In diesen Fällen läßt sich das Integral von $ \mbox{$f$}$ über $ \mbox{$I$}$ also mittels iterierter Integration berechnen. Im Falle der Existenz ist demzufolge
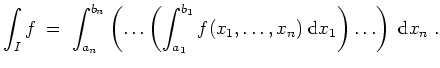
$ \mbox{$\displaystyle \int_I f \; = \; \int_{a_n}^{b_n} \left( \ldots \left( ... ...1, \ldots, x_n) \; \text{d} x_1 \right) \ldots \right) \; \text{d} x_n \; . $}$

Lebesguesche Nullmengen.

Eine Teilmenge $ \mbox{$M$}$ des $ \mbox{$\mathbb{R}^n$}$ heißt Lebesguesche Nullmenge, falls es für alle $ \mbox{$\varepsilon>0$}$ eine Folge von $ \mbox{$n$}$ -dimensionalen Quadern $ \mbox{$(I_k)_{k \in \mathbb{N}}$}$ so gibt, daß

Beispiele für Lebesguesche Nullmengen sind etwa

$ \mbox{$\bullet$}$
eine Menge von höchstens abzählbar vielen Punkten,
$ \mbox{$\bullet$}$
die Oberfläche einer Kugel, und
$ \mbox{$\bullet$}$
jede Hyperebene $ \mbox{$\{ x \in \mathbb{R}^n \vert a^\text{t} x = c \} \subseteq \mathbb{R}^n$}$ mit $ \mbox{$a \in \mathbb{R}^n\setminus\{ 0 \}$}$ und $ \mbox{$c \in \mathbb{R}$}$ .

Integration über beschränkte Mengen.

Es seien $ \mbox{$M \subseteq \mathbb{R}^n$}$ beschränkt und $ \mbox{$f:M \to \mathbb{R}$}$ eine Funktion. Wir definieren die Funktion

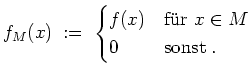
$ \mbox{$\displaystyle f_M(x) \; :=\; \begin{cases} f(x) & \text{f\uml ur {$\mbox{$x \in M$}$}}\\ 0 & \text{sonst}\; . \\ \end{cases}$}$

Es sei $ \mbox{$I$}$ ein $ \mbox{$n$}$ -dimensionaler Quader mit $ \mbox{$M \subseteq I$}$ . Die Funktion $ \mbox{$f$}$ heißt (Riemann-) integrierbar auf $ \mbox{$M$}$ , falls $ \mbox{$f_M$}$ integrierbar auf $ \mbox{$I$}$ ist. Dann heißt

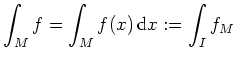
$ \mbox{$\displaystyle \int_M f = \int_M f(x) \, \text{d} x :=\int_I f_M $}$
das (Riemann-) Integral von $ \mbox{$f$}$ über $ \mbox{$M$}$ .

Meßbare Mengen.

Die Menge $ \mbox{$M$}$ heißt (Jordan-) meßbar, falls die konstante Funktion $ \mbox{$1$}$ integrierbar über $ \mbox{$M$}$ ist, und dann heißt

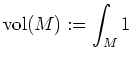
$ \mbox{$\displaystyle \text{vol}(M) := \int_M 1 $}$
der (Jordan-) Inhalt von $ \mbox{$M$}$ .

Zum Beispiel ist ein $ \mbox{$n$}$ -dimensionaler Quader meßbar, und sein Jordaninhalt stimmt mit seinem oben eingeführten Volumen überein.

Eine meßbare Lebesguesche Nullmenge $ \mbox{$M$}$ hat $ \mbox{$\text{vol}(M)=0$}$ .

Meßbarkeitskriterium. Eine beschränkte Menge $ \mbox{$M \subseteq \mathbb{R}^n$}$ ist genau dann meßbar, wenn die Menge der Randpunkte von $ \mbox{$M$}$ eine Lebesguesche Nullmenge ist.

Dabei heißt $ \mbox{$x \in \mathbb{R}^n$}$ ein Randpunkt von $ \mbox{$M$}$ , wenn $ \mbox{$x$}$ ein Berührpunkt von $ \mbox{$M$}$ , jedoch kein innerer Punkt von $ \mbox{$M$}$ ist. Mit anderen Worten, jede Umgebung von $ \mbox{$x$}$ enthält sowohl Punkte von $ \mbox{$M$}$ als auch vom Komplement von $ \mbox{$M$}$ .

Das Lebesguesche Integrabilitätskriterium.

Sei $ \mbox{$M \subseteq \mathbb{R}^n$}$ meßbar. Das Lebesguesche Integrabilitätskriterium besagt, daß eine beschränkte Funktion $ \mbox{$f:M \to \mathbb{R}$}$ genau dann integrierbar auf $ \mbox{$M$}$ ist, wenn die Menge ihrer Unstetigkeitspunkte auf $ \mbox{$M$}$ eine Lebesguesche Nullmenge ist.

Insbesondere sind stetige Funktionen auf meßbaren Mengen integrierbar.

Iterierte Integration, der Satz von Fubini und das Cavalierische Prinzip.

Es sei $ \mbox{$M \subseteq \mathbb{R}^n$}$ beschränkt und $ \mbox{$1 \leq m \leq n-1$}$ . Für jedes $ \mbox{$x \in \mathbb{R}^m$}$ sei

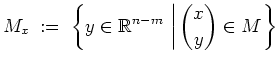
$ \mbox{$\displaystyle M_x \; :=\; \left\{ y \in \mathbb{R}^{n-m} \, \left\vert \, {x \choose y} \in M \right. \right\} $}$
der $ \mbox{$x$}$ -Schnitt von $ \mbox{$M$}$ , und
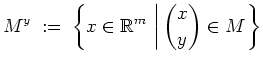
$ \mbox{$\displaystyle M^y \; :=\; \left\{ x \in \mathbb{R}^{m} \, \left\vert \, {x \choose y} \in M \right. \right\} $}$
der $ \mbox{$y$}$ -Schnitt von $ \mbox{$M$}$ .

Ferner sei 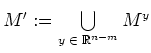$ \mbox{$M' := \bigcup\limits_{y \;\in\;\mathbb{R}^{n-m}} M^y$}$ und $ \mbox{$M'' := \bigcup\limits_{x\;\in\;\mathbb{R}^{m}} M_x$}$ . Anschaulich gesprochen ist $ \mbox{$M'$}$ die Projektion von $ \mbox{$M$}$ auf die $ \mbox{$(x_1,\ldots,x_m)$}$ -Ebene, und $ \mbox{$M''$}$ die Projektion von $ \mbox{$M$}$ auf die $ \mbox{$(x_{m+1},\ldots,x_n)$}$ -Ebene.

Der Satz von Fubini besagt nun, daß einerseits

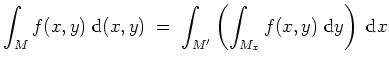
$ \mbox{$\displaystyle \int_M f(x,y) \; \text{d}(x,y) \; = \; \int_{M'} \left(\int_{M_x} f(x,y) \; \text{d} y\right) \; \text{d} x $}$
gilt, falls alle auftretenden Integrale existieren, und daß andererseits
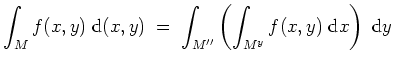
$ \mbox{$\displaystyle \int_M f(x,y) \; \text{d}(x,y) \; = \; \int_{M''} \left(\int_{M^y} f(x,y) \; \text{d} x\right) \; \text{d} y $}$
falls wiederum alle auftretenden Integrale existieren. In diesen Fällen läßt sich das Integral von $ \mbox{$f$}$ über $ \mbox{$M$}$ also mittels iterierter Integration berechnen.

Insbesondere erhalten wir mit $ \mbox{$f(x,y) = 1$}$ konstant das Cavalierische Prinzip, welches besagt, daß

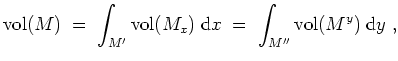
$ \mbox{$\displaystyle \text{vol}(M) \; =\; \int_{M'} \text{vol}(M_x) \; \text{d} x \;=\; \int_{M''} \text{vol}(M^y) \; \text{d} y \; , $}$
falls alle auftretenden Integrale existieren.

Regeln.

Es seien $ \mbox{$M \subseteq \mathbb{R}^n$}$ ein beschränkte Menge, $ \mbox{$f, g$}$ integrierbar auf $ \mbox{$M$}$ und $ \mbox{$\alpha, \beta \in \mathbb{R}$}$ . Dann gelten folgende Regeln.

1.
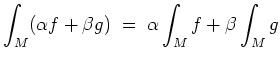$ \mbox{$\displaystyle \int_M (\alpha f + \beta g) \; =\; \alpha \int_M f + \beta \int_M g$}$ (Linearität).
2.
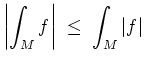$ \mbox{$\displaystyle \left\vert \int_M f \right\vert \;\leq\; \int_M \vert f\vert$}$ (Dreiecksungleichung).
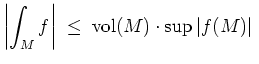Ist zusätzlich $ \mbox{$M$}$ meßbar, so ist $ \mbox{$\displaystyle \left\vert \int_M f \right\vert \;\leq\; \text{vol}(M)\cdot\sup \vert f(M)\vert\;$}$ (Prismenungleichung).
3.
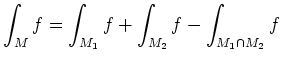Es ist $ \mbox{$\displaystyle \int_M f = \int_{M_1} f + \int_{M_2} f - \int_{M_1 \cap M_2} f$}$ , sofern $ \mbox{$M=M_1 \cup M_2$}$ und sofern $ \mbox{$f$}$ integrierbar ist über $ \mbox{$M_1$}$ , $ \mbox{$M_2$}$ und $ \mbox{$M_1 \cap M_2$}$ .
4.
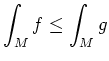$ \mbox{$\displaystyle \int_M f \leq \int_M g$}$ , falls $ \mbox{$f \leq g$}$ auf $ \mbox{$M$}$ gilt.
5.
Falls $ \mbox{$M$}$ eine Lebesguesche Nullmenge ist, so ist $ \mbox{$\int_M f = 0$}$ .
6.
Es seien $ \mbox{$M$}$ meßbar, $ \mbox{$y\in\mathbb{R}^n$}$ , $ \mbox{$\alpha>0$}$ und $ \mbox{$\tilde{M}=\{y+\alpha x\; \vert\; x\in M\}$}$ die um den Vektor $ \mbox{$y$}$ verschobene und um den Faktor $ \mbox{$\alpha$}$ gestreckte Menge. Dann gilt $ \mbox{$\text{vol}(\tilde{M})=\alpha^n\;\text{vol}(M)$}$ . (Dies ist ein einfacher Spezialfall der mehrdimensionalen Substitutionsregel.)

Der Schwerpunkt und die erste Guldinsche Regel.

Es sei $ \mbox{$M \subseteq \mathbb{R}^n$}$ eine meßbare Menge mit $ \mbox{$\text{vol}(M)>0$}$ . Dann heißt der Punkt $ \mbox{$(s_1,\ldots,s_n)^\text{t}\in\mathbb{R}^n$}$ mit den Koordinaten

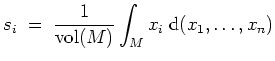
$ \mbox{$\displaystyle s_i \;=\; \dfrac{1}{\text{vol}(M)}\int_M x_i\;\text{d}(x_1,\ldots,x_n) $}$
der Schwerpunkt von $ \mbox{$M$}$ .

Es sei nun $ \mbox{$M\subseteq\mathbb{R}_{\geq 0}\times\mathbb{R}$}$ eine meßbare Menge mit Schwerpunkt $ \mbox{$(s_1,s_2)^\text{t}$}$ . Es sei $ \mbox{$R$}$ der aus $ \mbox{$M$}$ entstehende Rotationskörper bei Drehung um die $ \mbox{$y$}$ -Achse, definiert durch

$ \mbox{$\displaystyle R \; :=\; \{(x,y,z)^\text{t}\in\mathbb{R}^3\; \vert\; (\sqrt{x^2 + z^2},\, y)^\text{t}\in M\}\;. $}$
Nach der ersten Guldinschen Regel ist der Inhalt von $ \mbox{$R$}$ gegeben durch

$ \mbox{$\displaystyle \text{vol}(R) \;=\; \text{vol}(M)\cdot 2\pi s_1\;. $}$
Mit anderen Worten, der Inhalt des Rotationskörpers $ \mbox{$R$}$ ist gleich dem Inhalt der Fläche $ \mbox{$M$}$ , multipliziert mit der Länge des zurückgelegten Weges des Flächenschwerpunktes bei einmaliger Rotation um die $ \mbox{$y$}$ -Achse.