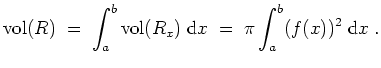
Alternativ kann der Inhalt auch mit der ersten Guldinschen Regel berechnet werden.
Es sei dazu
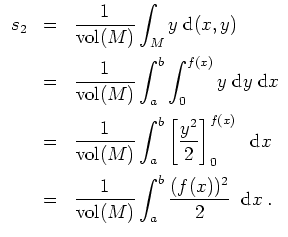
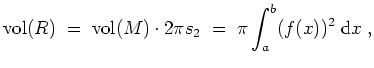
Es sei
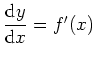 also
also
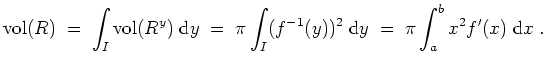
Alternativ kann der Inhalt auch mit der ersten Guldinschen Regel berechnet werden.
Es sei dazu
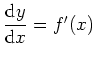 zu
zu
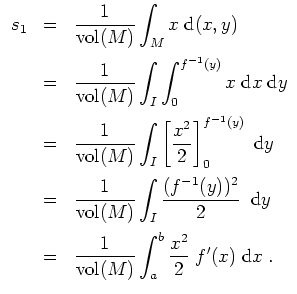
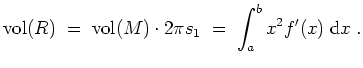
![$ \mbox{$\displaystyle
\pi\int_0^h(f(x))^2\;\text{d}x
\;=\; \pi\int_0^h \dfrac{...
...\; \pi\left[\dfrac{r^2x^3}{3h^2}\right]_0^h
\;=\; \dfrac{1}{3}\;\pi r^2 h\;,
$}$](img37.png)
![$ \mbox{$\displaystyle
\pi\int_{-r}^r(f(x))^2\;\text{d}x
\;=\; \pi\int_{-r}^r(r...
...t{d}x
\;=\; \pi\left[r^2x-x^3/3\right]_{-r}^r
\;=\; \dfrac{4}{3}\;\pi r^3\;.
$}$](img39.png)
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\pi\displaystyle\int_{-1}^1(f(x))^2\;...
...^{-2x}+4x}{8}\right]_{-1}^1
\;=\; \pi\;\dfrac{e^2-e^{-2}+4}{4}\;.
\end{array}$}$](img40.png)
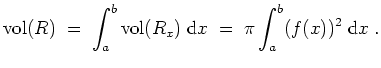
Alternativ kann der Inhalt auch mit der ersten Guldinschen Regel berechnet werden.
Es sei dazu
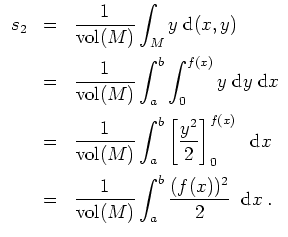
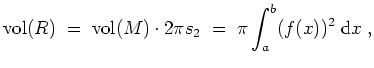
Es sei
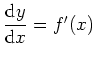 also
also
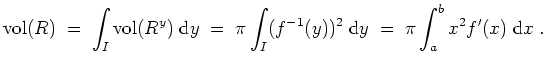
Alternativ kann der Inhalt auch mit der ersten Guldinschen Regel berechnet werden.
Es sei dazu
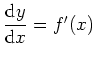 zu
zu
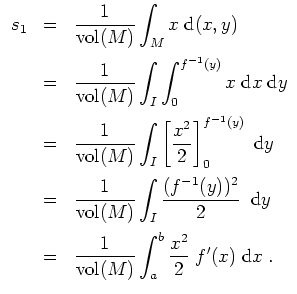
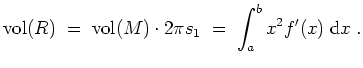
![$ \mbox{$\displaystyle
\pi\int_0^h(f(x))^2\;\text{d}x
\;=\; \pi\int_0^h \dfrac{...
...\; \pi\left[\dfrac{r^2x^3}{3h^2}\right]_0^h
\;=\; \dfrac{1}{3}\;\pi r^2 h\;,
$}$](img37.png)
![$ \mbox{$\displaystyle
\pi\int_{-r}^r(f(x))^2\;\text{d}x
\;=\; \pi\int_{-r}^r(r...
...t{d}x
\;=\; \pi\left[r^2x-x^3/3\right]_{-r}^r
\;=\; \dfrac{4}{3}\;\pi r^3\;.
$}$](img39.png)
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\pi\displaystyle\int_{-1}^1(f(x))^2\;...
...^{-2x}+4x}{8}\right]_{-1}^1
\;=\; \pi\;\dfrac{e^2-e^{-2}+4}{4}\;.
\end{array}$}$](img40.png)