Lösung.

Für $ \mbox{$z\in[0,h]$}$ ergibt sich der $ \mbox{$z$}$ -Schnitt von $ \mbox{$K$}$ zu

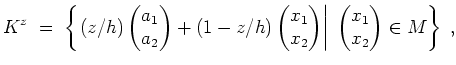
$ \mbox{$\displaystyle K^z \;=\; \left\{\left.(z/h)\begin{pmatrix}a_1\\ a_2\en... ...atrix}\right\vert\; \begin{pmatrix}x_1\\ x_2\end{pmatrix}\in M\right\}\;, $}$
denn in der Darstellung
$ \mbox{$\displaystyle K \;=\; \left\{\left.\lambda\begin{pmatrix}a_1\\ a_2\\ ... ...t\; \lambda\in[0,1],\; \begin{pmatrix}x_1\\ x_2\end{pmatrix}\in M\right\} $}$
sind die Punkte mit dritter Koordinate $ \mbox{$z$}$ gerade gegeben durch $ \mbox{$\lambda=z/h$}$ .

Die Menge $ \mbox{$K^z$}$ entsteht aus $ \mbox{$M$}$ durch eine Verschiebung und eine Streckung um den Faktor $ \mbox{$(1-z/h)$}$ . Daher gilt

$ \mbox{$\displaystyle \text{vol}(K^z) \;=\; (1-z/h)^2\;\text{vol}(M)\;. $}$

Ferner ist $ \mbox{$K^z=\emptyset$}$ für $ \mbox{$z\notin[0,h]$}$ . Also ist die Projektion von $ \mbox{$K$}$ auf die $ \mbox{$z$}$ -Achse gegeben durch $ \mbox{$K''=[0,h]$}$ . Nach dem Prinzip von Cavalieri folgt

$ \mbox{$\displaystyle \begin{array}{rcl} \text{vol}(K) &=& \displaystyle\int_0... ...right]_0^h\vspace*{2mm}\\ &=& \dfrac{1}{3}\;h\;\text{vol}(M)\;. \end{array}$}$

Kurz, das Volumen des Kegels ist gleich $ \mbox{$\dfrac{1}{3}$}$ $ \mbox{$\cdot$}$ Höhe $ \mbox{$\cdot$}$ Grundfläche.