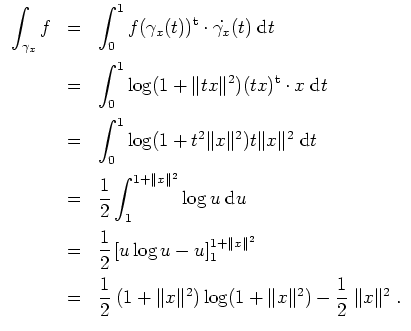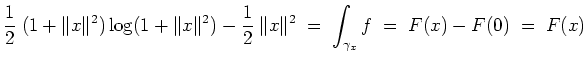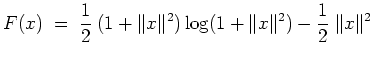- Es gilt
Also folgt
und aus Symmetriegründen folgen
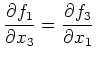 und
und
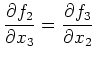 . Also erfüllt
. Also erfüllt
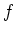 die Integrabilitätsbedingungen
auf
die Integrabilitätsbedingungen
auf
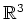 . Nach dem zweiten Hauptsatz für Kurvenintegrale ist das Vektorfeld
. Nach dem zweiten Hauptsatz für Kurvenintegrale ist das Vektorfeld
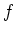 mithin konservativ, da das Gebiet
mithin konservativ, da das Gebiet
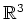 sternförmig ist.
sternförmig ist.
- Eine Parametrisierung von
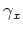 lautet
Also gilt
lautet
Also gilt
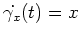 für alle
für alle
![$ \mbox{$t\in[0,1]$}$](img10.png) . Mit der Substitution
. Mit der Substitution
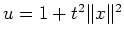 wird
wird
- Nach Aufgabenteil 1. besitzt das Vektorfeld
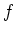 eine Stammfunktion
eine Stammfunktion
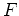 . Wir können o.E.
. Wir können o.E.
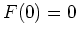 annehmen,
da die Subtraktion einer Konstanten nichts an der Ableitung ändert. Mit dem ersten Hauptsatz für Kurvenintegrale und
Aufgabenteil 2. folgt dann
für alle
annehmen,
da die Subtraktion einer Konstanten nichts an der Ableitung ändert. Mit dem ersten Hauptsatz für Kurvenintegrale und
Aufgabenteil 2. folgt dann
für alle
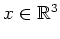 . Somit ist
eine Stammfunktion von
. Somit ist
eine Stammfunktion von
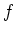 .
.
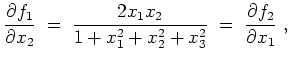
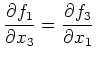 und
und
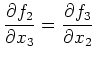 . Also erfüllt
. Also erfüllt
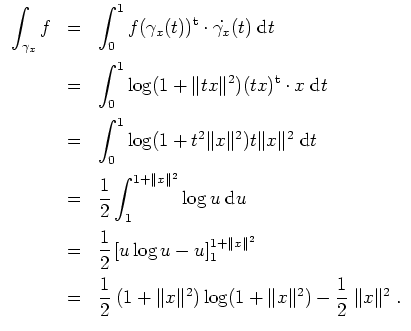
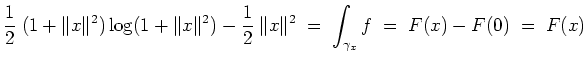
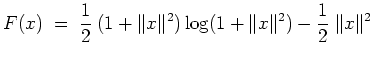
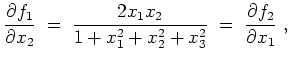
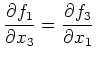 und
und
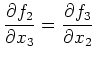 . Also erfüllt
. Also erfüllt