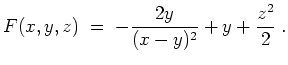Es wird
und
Also erfüllt
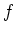 genau dann die Integrabilitätsbedingungen, wenn
genau dann die Integrabilitätsbedingungen, wenn
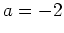 .
.
Man kann eine Stammfunktion
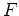 in diesem Falle wie folgt berechnen.
in diesem Falle wie folgt berechnen.
für eine Funktion
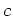 , die nur von
, die nur von
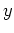 und
und
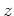 abhängt. Weiter gilt
für eine Funktion
abhängt. Weiter gilt
für eine Funktion
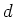 , die nur von
, die nur von
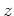 abhängt. Schließlich gilt
Wir können also
abhängt. Schließlich gilt
Wir können also
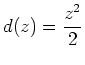 wählen und erhalten als Stammfunktion
Der maximale Definitionsbereich ist dabei
wählen und erhalten als Stammfunktion
Der maximale Definitionsbereich ist dabei
 . Man beachte, daß das Gebiet
. Man beachte, daß das Gebiet
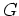 nicht
einfach zusammenhängend ist (also auch nicht sternförmig). Trotzdem gilt
nicht
einfach zusammenhängend ist (also auch nicht sternförmig). Trotzdem gilt
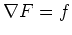 auf dem gesamten Gebiet
auf dem gesamten Gebiet
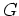 . Man hätte aber
auch eine Stammfunktion erhalten, wenn man auf
. Man hätte aber
auch eine Stammfunktion erhalten, wenn man auf
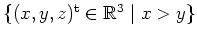 noch eine beliebige Konstante zu
noch eine beliebige Konstante zu
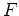 addiert hätte.
addiert hätte.
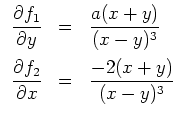
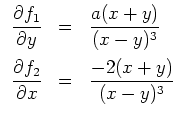
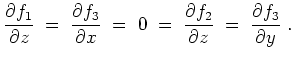
![]() genau dann die Integrabilitätsbedingungen, wenn
genau dann die Integrabilitätsbedingungen, wenn
![]() .
.
![]() in diesem Falle wie folgt berechnen.
in diesem Falle wie folgt berechnen.
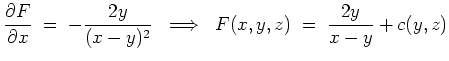
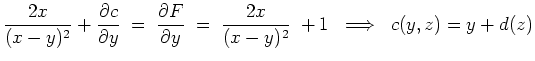
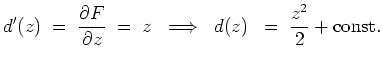
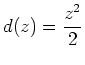 wählen und erhalten als Stammfunktion
wählen und erhalten als Stammfunktion