Wir geben drei Lösungsmöglichkeiten an.
- Wir wollen mit dem zweiten Hauptsatz für Kurvenintegrale beweisen, daß
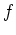 konservativ ist.
Es gilt
Also ist
Aus Symmetriegründen ist daher auch
Also erfüllt
konservativ ist.
Es gilt
Also ist
Aus Symmetriegründen ist daher auch
Also erfüllt
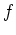 die Integrabilitätsbedingungen. Da das Gebiet
die Integrabilitätsbedingungen. Da das Gebiet
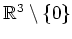 einfach zusammenhängend ist, ist das Vektorfeld
einfach zusammenhängend ist, ist das Vektorfeld
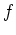 nach dem zweiten Hauptsatz für Kurvenintegral konservativ.
Da der Weg
nach dem zweiten Hauptsatz für Kurvenintegral konservativ.
Da der Weg
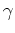 geschlossen ist, folgt also
geschlossen ist, folgt also
- Wir berechnen direkt eine Stammfunktion von
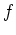 . Es gilt
für
. Es gilt
für
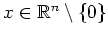 , wie man direkt verifiziert.
Ist
, wie man direkt verifiziert.
Ist
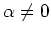 , so folgt mit der Kettenregel
Speziell gilt also mit
, so folgt mit der Kettenregel
Speziell gilt also mit
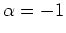 Also ist die Funktion
eine Stammfunktion von
Also ist die Funktion
eine Stammfunktion von
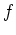 . Mithin ist das Vektorfeld
. Mithin ist das Vektorfeld
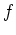 konservativ, und es folgt
konservativ, und es folgt
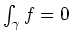 , da der Weg
, da der Weg
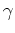 geschlossen ist.
geschlossen ist.
- Wir berechnen
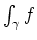 direkt mit der Definition. Es wird mit der Substitution
direkt mit der Definition. Es wird mit der Substitution
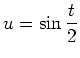 und
und
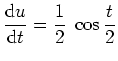
Skizze des Vivianischen Fensters.
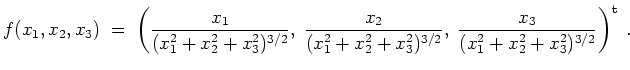
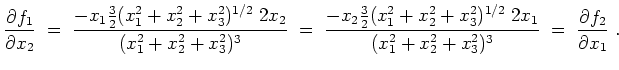
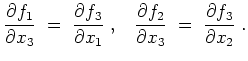
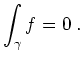
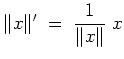
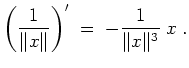
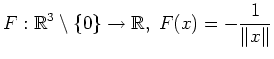
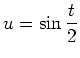 und
und
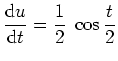
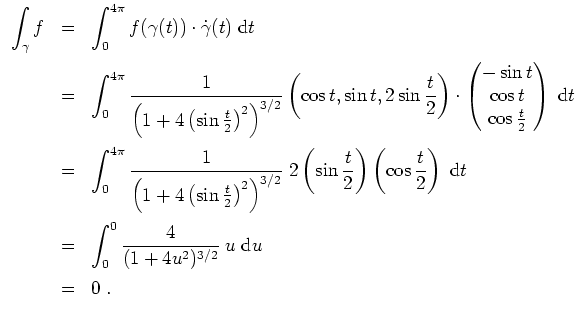
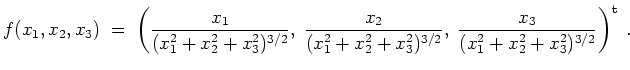
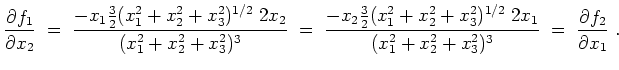
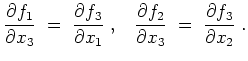
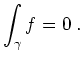
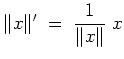
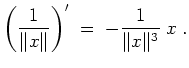
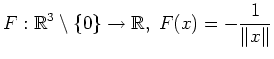
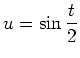 und
und
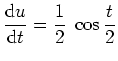
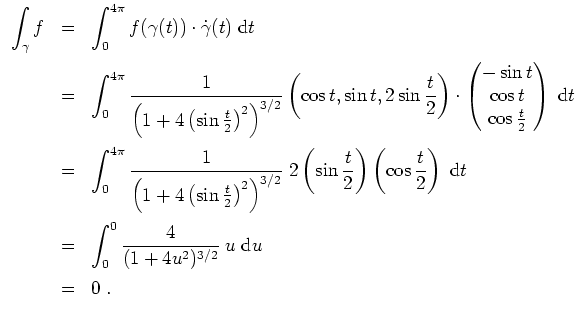
![\includegraphics[width = 8cm]{s2.eps}](img20.png)