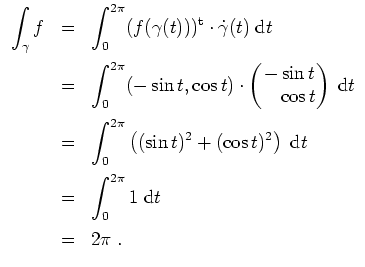
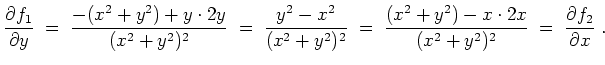
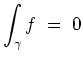
Also ist das Vektorfeld
![]() nicht konservativ.
nicht konservativ.
Bemerkung: Dies wiederspricht nicht dem zweiten Hauptsatz für Kurvenintegrale, denn das Gebiet
![]() ist nicht einfach zusammenhängend (und insbesondere nicht sternförmig). Es hat ein ,,Loch``bei
ist nicht einfach zusammenhängend (und insbesondere nicht sternförmig). Es hat ein ,,Loch``bei
![]() .
.
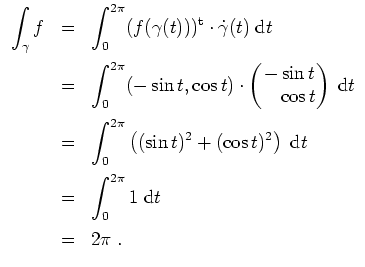
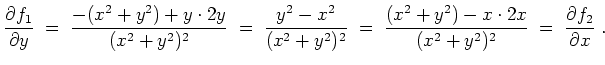
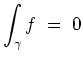
Also ist das Vektorfeld
![]() nicht konservativ.
nicht konservativ.
Bemerkung: Dies wiederspricht nicht dem zweiten Hauptsatz für Kurvenintegrale, denn das Gebiet
![]() ist nicht einfach zusammenhängend (und insbesondere nicht sternförmig). Es hat ein ,,Loch``bei
ist nicht einfach zusammenhängend (und insbesondere nicht sternförmig). Es hat ein ,,Loch``bei
![]() .
.