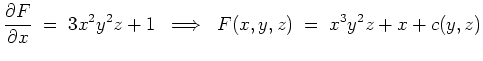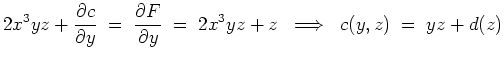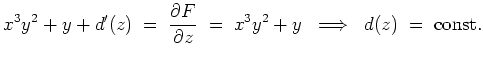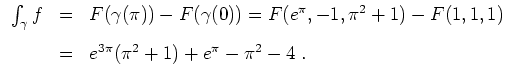Hier erfüllt
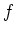 die Integrabilitätsbedingungen, denn es gilt
Ferner ist der Definitionsbereich von
die Integrabilitätsbedingungen, denn es gilt
Ferner ist der Definitionsbereich von
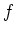 ein sternförmiges, also einfach zusammenhängendes Gebiet, nämlich
ein sternförmiges, also einfach zusammenhängendes Gebiet, nämlich
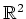 .
Nach dem zweiten Hauptsatz für Kurvenintegrale ist das Vektorfeld
.
Nach dem zweiten Hauptsatz für Kurvenintegrale ist das Vektorfeld
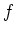 also konservativ.
also konservativ.
Wir wollen nun eine Stammfunktion
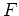 von
von
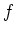 berechnen. Hierzu iteriert man ,,partielles Aufleiten``.
berechnen. Hierzu iteriert man ,,partielles Aufleiten``.
Zunächst wird
mit einer stetig differenzierbaren Funktion
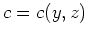 , die nicht von
, die nicht von
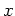 abhängt.
abhängt.
Weiter gilt
für eine stetig differenzierbare Funktion
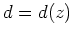 , die weder von
, die weder von
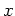 noch von
noch von
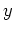 abhängt.
abhängt.
Schließlich gilt
Wir können also
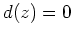 wählen und erhalten als eine Stammfunktion
Diese ist nur bis auf eine additive Konstante bestimmt.
wählen und erhalten als eine Stammfunktion
Diese ist nur bis auf eine additive Konstante bestimmt.
Nach dem ersten Hauptsatz für Kurvenintegrale wird nun
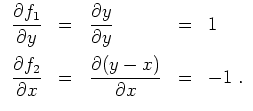
![]() längs
längs
![]() ergibt sich zu
ergibt sich zu
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle\int_\gamma f
&=& \displ...
...}-\dfrac{t^3}{3}\right]_0^2\vspace*{2mm}\\
&=& \dfrac{16}{3}\;.
\end{array}$}$](img4.png)
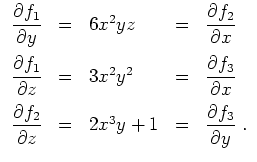
![]() von
von
![]() berechnen. Hierzu iteriert man ,,partielles Aufleiten``.
berechnen. Hierzu iteriert man ,,partielles Aufleiten``.