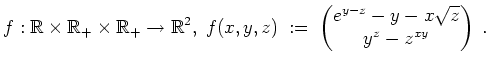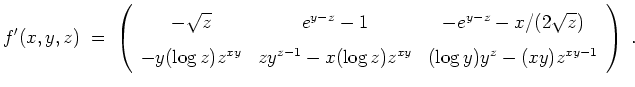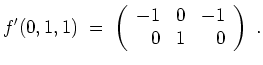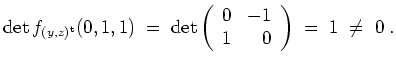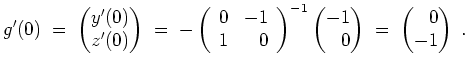Schreibe
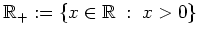 .
.
- Sei
Es wird
Speziell wird
Also ist
Nach dem Satz über implizite Funktionen läßt sich das Gleichungssystem
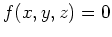 lokal um den Punkt
lokal um den Punkt
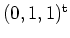 nach
nach
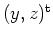 auflösen. Also gibt es Umgebungen
auflösen. Also gibt es Umgebungen
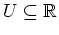 von
von
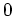 und
und
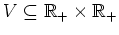 von
von
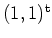 sowie genau eine Funktion
sowie genau eine Funktion
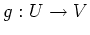 ,
,
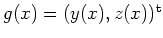 so, daß
so, daß
-
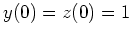 ,
,
-
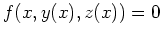 für alle
für alle
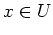 ,
,
-
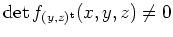 für alle
für alle
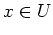 und
und
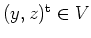 .
.
- Für
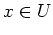 erhalten wir
also für
erhalten wir
also für
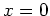
![]() .
.