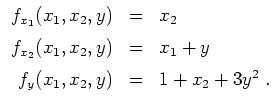
-
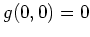 ,
,
-
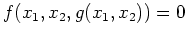 für alle
für alle
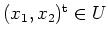 ,
,
-
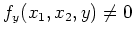 für alle
für alle
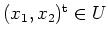 und
und
 .
.
Insbesondere wird
Eine weitere Anwendung der Kettenregel ergibt
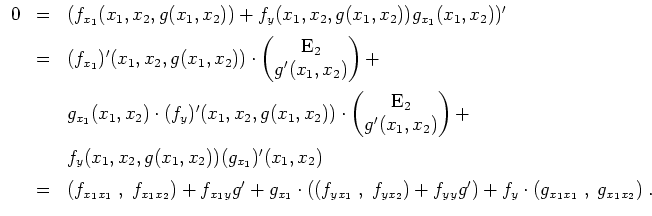
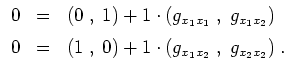
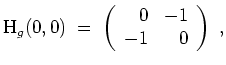
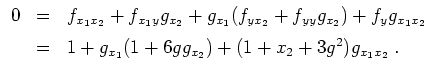
Hier eine Skizze der Lösungsmenge von
![]() . Man erkennt einen Sattelpunkt bei
. Man erkennt einen Sattelpunkt bei
![]() .
.
![\includegraphics[width = 12cm]{s2.eps}](img34.png)
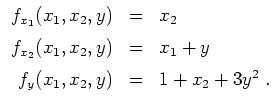
Insbesondere wird
Eine weitere Anwendung der Kettenregel ergibt
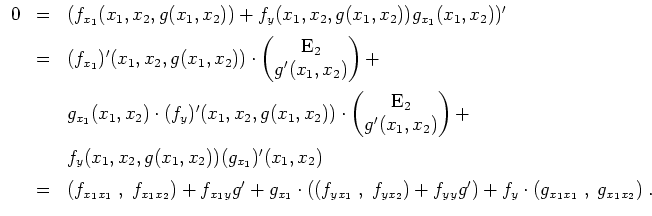
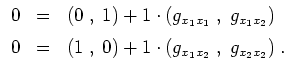
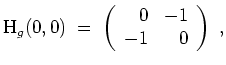
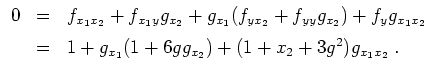
Hier eine Skizze der Lösungsmenge von
![]() . Man erkennt einen Sattelpunkt bei
. Man erkennt einen Sattelpunkt bei
![]() .
.
![\includegraphics[width = 12cm]{s2.eps}](img34.png)