Lösung.

Es wird
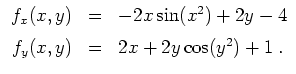
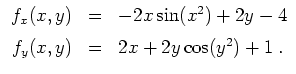
$ \mbox{$\displaystyle \begin{array}{rcl} f_x(x,y) &=& -2x\sin(x^2)+2y-4 \vspace*{2mm}\\ f_y(x,y) &=& 2x+2y\cos(y^2)+1 \;. \end{array}$}$
Also ist $ \mbox{$f$}$ zweimal stetig differenzierbar, $ \mbox{$f(0,0)=0$}$ und $ \mbox{$f_y(0,0)=1\ne 0$}$ .

Nach dem Satz über implizite Funktionen ist die Gleichung $ \mbox{$f(x,y)=0$}$ um den Punkt $ \mbox{$(0,0)^\text{t}$}$ lokal eindeutig nach $ \mbox{$y$}$ auflösbar. Es gibt also Umgebungen $ \mbox{$U_0,\, V_0\,\subseteq\,\mathbb{R}$}$ von $ \mbox{$0$}$ und (genau) eine stetig differenzierbare Funktion $ \mbox{$g:U_0\to V_0$}$ so, daß

Es wird

$ \mbox{$\displaystyle g'(x) \;=\; -f_y(x,g(x))^{-1} f_x(x,g(x)) \;=\; -(2x+2y\cos(y^2)+1)^{-1} (-2x\sin(x^2)+2y-4) $}$
für alle $ \mbox{$x\in U_0$}$ . Da insbesondere $ \mbox{$f_y(x,g(x))^{-1} \ne 0$}$ für alle $ \mbox{$x\in U_0$}$ ist, ist $ \mbox{$g$}$ zweimal stetig differenzierbar.

Als Wert bei $ \mbox{$x = 0$}$ erhalten wir $ \mbox{$g'(0) = 4$}$ wegen $ \mbox{$y = 0$}$ dort.

Berechnen wir die zweite Ableitung. Mit der Kettenregel ergibt sich

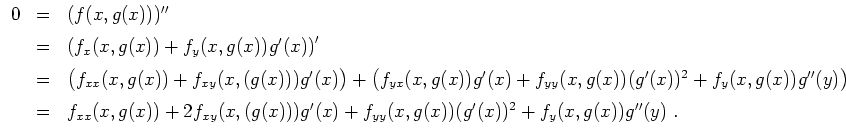
$ \mbox{$\displaystyle \begin{array}{rcl} 0 & = & (f(x,g(x)))''\vspace*{2mm}\\... ...x)))g'(x) + f_{yy}(x,g(x))(g'(x))^2 + f_y(x,g(x))g''(y) \; . \\ \end{array}$}$
Es sind
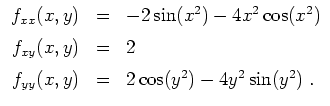
$ \mbox{$\displaystyle \begin{array}{rcl} f_{xx}(x,y) &=& -2\sin(x^2)-4x^2\cos(... ...& 2 \vspace*{2mm}\\ f_{yy}(x,y) &=& 2\cos(y^2)-4y^2\sin(y^2)\;. \end{array}$}$
Setzen wir dies in obige Gleichung für $ \mbox{$(x,y)^\text{t} = (0,0)^\text{t}$}$ ein, so erhalten wir
$ \mbox{$\displaystyle 0 \;=\; 0 + 2\cdot 2\cdot 4 + 2\cdot 4^2 + 1\cdot g''(0)\; , $}$
und also $ \mbox{$g''(0) = -48$}$ .

Skizze der Lösungskurve von $ \mbox{$f(x,y)=0$}$ .

\includegraphics[width = 12cm]{s1.eps}

Skizze von $ \mbox{$f(x,y)=0$}$ näher bei $ \mbox{$(0,0)^\text{t}$}$ .

\includegraphics[width = 8cm]{s1-2.eps}