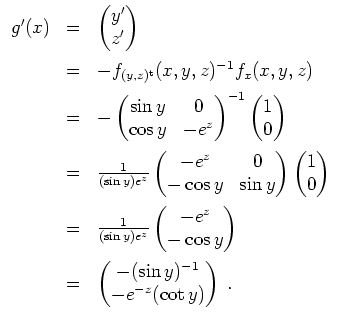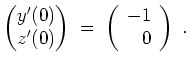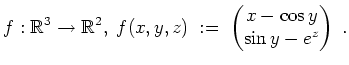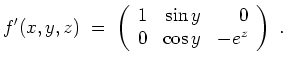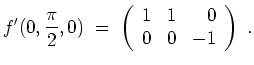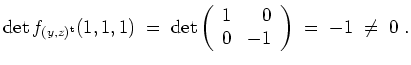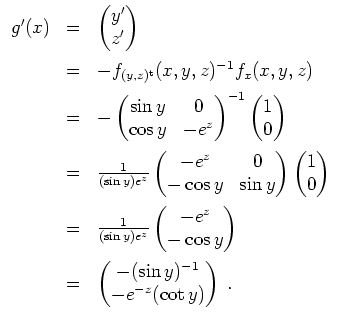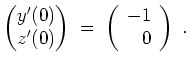- 1.
- Es sei
Es wird
Speziell ergibt sich
Also ist
Nach dem Satz über implizite Funktionen läßt sich
das Gleichungssystem
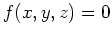 lokal um den Punkt
lokal um den Punkt
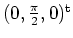 nach
nach
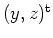 auflösen.
auflösen.
- 2.
- Nach 1. gibt es also Umgebungen
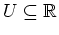 von
von
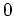 und
und
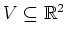 von
von
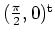 sowie genau eine
stetig differenzierbare Funktion
sowie genau eine
stetig differenzierbare Funktion
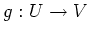 ,
,
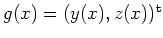 so, daß
so, daß
-
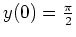 ,
,
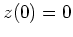 ,
,
-
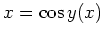 und
und
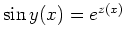 für alle
für alle
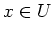 ,
,
-
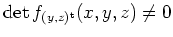 für alle
für alle
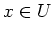 und
und
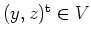 .
.
Es wird
Speziell wird
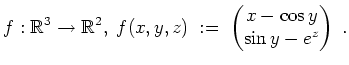
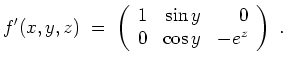
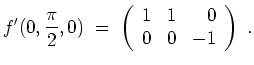
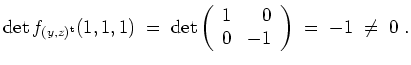
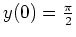 ,
,
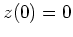 ,
,
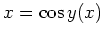 und
und
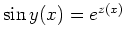 für alle
für alle
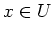 ,
,
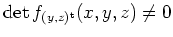 für alle
für alle
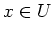 und
und
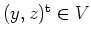 .
.