Lösung.

1.
Mit $ \mbox{$F := f - \lambda g$}$ und $ \mbox{$\lambda = (\lambda_1,\lambda_2)$}$ erhalten wir
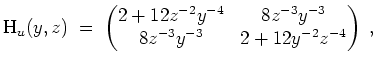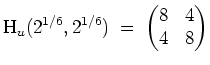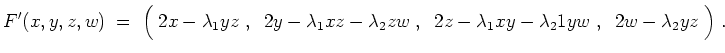
$ \mbox{$\displaystyle F'(x,y,z,w) \;=\; \Big(\; 2x - \lambda_1 yz\; ,\;\; 2y -... ...;\; 2z - \lambda_1 xy - \lambda_21 yw\; , \;\; 2w - \lambda_2 yz\;\Big)\; . $}$
Zusammen mit $ \mbox{$g = 0$}$ liefert dies das Gleichungssystem
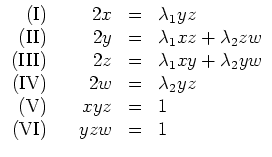
$ \mbox{$\displaystyle \begin{array}{rcrcl} \text{(I)} & & 2x & = & \lambda_1 y... ... \text{(V)} & & xyz & = & 1 \\ \text{(VI)} & & yzw & = & 1 \\ \end{array}$}$
zur Ermittlung der kritischen Punkte.

Aus (V, VI) folgt, daß $ \mbox{$x = w$}$ .

Aus (I, IV) ergeben sich $ \mbox{$\lambda_1 = \lambda_2 = \frac{2x}{yz}$}$ .

Aus (II, III) erhalten wir $ \mbox{$y^2 = z^2 = 2x^2$}$ , und also wegen $ \mbox{$(x,y,z,w)^\text{t}\in P$}$ auch $ \mbox{$y = z = 2^{1/2}x$}$ .

Aus (V) folgt schließlich $ \mbox{$x = 2^{-1/3}$}$ , und wir erhalten den kritischen Punkt

$ \mbox{$\displaystyle (2^{-1/3},2^{1/6},2^{1/6},2^{-1/3})^\text{t}\; . $}$

Da

$ \mbox{$\displaystyle g'(x,y,z,w) \;=\; \left[ \begin{array}{cccc} yz & xz & xy & 0 \\ 0 & zw & yw & yz \\ \end{array}\right] $}$
auf ganz $ \mbox{$P$}$ Rang $ \mbox{$2$}$ hat, ist der gefundene kritische Punkt regulär.

Da insbesondere

$ \mbox{$\displaystyle g'(2^{-1/3},2^{1/6},2^{1/6},2^{-1/3}) \;=\; \left[ \beg... ...-1/6} & 0 \\ 0 & 2^{-1/6} & 2^{-1/6} & 2^{1/3} \\ \end{array}\right]\; , $}$
können wir z.B.
$ \mbox{$\displaystyle \text{T}_g(2^{-1/3},2^{1/6},2^{1/6},2^{-1/3}) \;=\; \le... ...ray}{rr} 1 & 0 \\ 0 & 1 \\ 0 & -1 \\ -1 & 0 \\ \end{array}\right] $}$
wählen.

Allgemein ist

$ \mbox{$\displaystyle \text{H}_F(x,y,z,w) \;=\; \left[ \begin{array}{cccc} 2 ... ...da_2 y \\ 0 & -\lambda_2 z & -\lambda_2 y & 2 \\ \end{array}\right]\; . $}$
Speziell wird die relative Hessematrix am kritischen Punkt also zu
$ \mbox{$\displaystyle \begin{array}{rcl} \text{H}_{f;g}(2^{-1/3},2^{1/6},2^{1/... ... \begin{array}{rr} 4 & 0 \\ 0 & 8 \\ \end{array}\right]\; , \end{array}$}$
und ist somit positiv definit. Mithin liegt bei $ \mbox{$(2^{-1/3},2^{1/6},2^{1/6},2^{-1/3})^\text{t} \approx (0.7937,1.122,1.122,0.7937)^\text{t}$}$ ein lokales Minimum unter Nebenbedingung $ \mbox{$g = 0$}$ vor.

2.
Substitution von $ \mbox{$x = w = \frac{1}{yz}$}$ in $ \mbox{$f$}$ liefert die Funktion
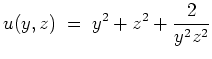
$ \mbox{$\displaystyle u(y,z) \;=\; y^2 + z^2 + \frac{2}{y^2 z^2} $}$
auf $ \mbox{$\tilde{P} := \{ (y,z)^\text{t}\in\mathbb{R}^2 \; \vert\; y > 0,\; z > 0\}$}$ .

Die Ableitung

$ \mbox{$\displaystyle u'(y,z) \;=\; (2y - 4z^{-2}y^{-3},\; 2z - 4y^{-2}z^{-3}) $}$
verschwindet auf $ \mbox{$\tilde{P}$}$ gerade bei $ \mbox{$z = y = 2^{1/6}$}$ .

Allgemein ist

$ \mbox{$\displaystyle \text{H}_u(y,z) \;=\; \begin{pmatrix}2 + 12 z^{-2} y^{-4} & 8z^{-3}y^{-3}\\ 8z^{-3}y^{-3} & 2 + 12 y^{-2} z^{-4}\end{pmatrix} \; , $}$
so daß sich im kritischen Punkt $ \mbox{$(2^{1/6},2^{1/6})$}$ die positiv definite Hessematrix
$ \mbox{$\displaystyle \text{H}_u(2^{1/6},2^{1/6}) \;=\; \begin{pmatrix}8&4\\ 4&8\end{pmatrix} $}$
ergibt. Somit liegt bei $ \mbox{$(2^{1/6},2^{1/6})$}$ ein lokales Minimum vor, in Übereinstimmung mit (1).

Man beachte, daß der zweite Lösungsweg nur gangbar ist, da sich in den Nebenbedingungen Variablen rechnerisch isolieren lassen.