Es ist
und demzufolge
Ferner berechnen wir
Aus der notwendigen Bedingung erhalten wir
und erhalten als einzigen kritischen Punkt
Die Hessematrix ist als Diagonalmatrix mit positiven Diagonaleinträgen positiv definit für alle
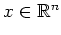 , so daß wir aus dem Satz von Taylor
ein
, so daß wir aus dem Satz von Taylor
ein
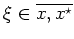 mit
erhalten. Gleichheit tritt genau dann ein, wenn
mit
erhalten. Gleichheit tritt genau dann ein, wenn
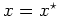 ist.
ist.
Dies zeigt, daß
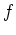 bei
bei
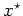 ein globales Minimum annimmt.
ein globales Minimum annimmt.
Bemerkung. Interpretiert man die Größen
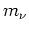 als Massen von Massenpunkten an den Orten
als Massen von Massenpunkten an den Orten
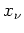 , so befindet sich das globale
Minimum in deren Schwerpunkt
, so befindet sich das globale
Minimum in deren Schwerpunkt
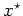 .
.
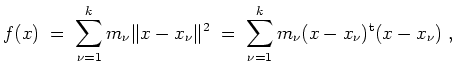
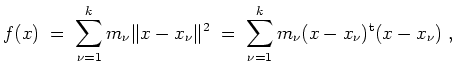
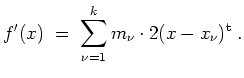
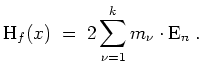
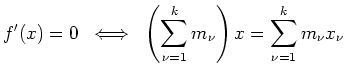
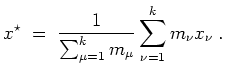
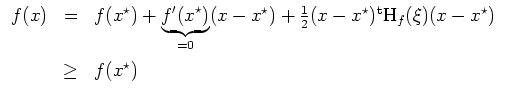
![]() bei
bei
![]() ein globales Minimum annimmt.
ein globales Minimum annimmt.
![]() als Massen von Massenpunkten an den Orten
als Massen von Massenpunkten an den Orten
![]() , so befindet sich das globale
Minimum in deren Schwerpunkt
, so befindet sich das globale
Minimum in deren Schwerpunkt
![]() .
.