Es ist die Jacobimatrix
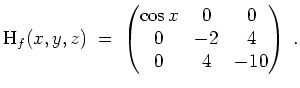
Die kritischen Punkte ermitteln sich aus
![]() , d.h. aus dem Gleichungssystem
, d.h. aus dem Gleichungssystem
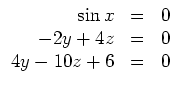
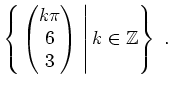
Ist
![]() gerade, so ist
gerade, so ist
![]() , und folglich
, und folglich
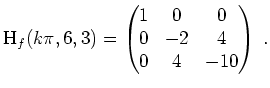
Alternativ kann man die Matrix auch durch beidseitige Gaußumformungen zu
 umformen, und erkennt auch so, daß eine
indefinite Matrix vorliegt.
umformen, und erkennt auch so, daß eine
indefinite Matrix vorliegt.
Folglich besitzt
![]() einen Sattelpunkt an den Stellen
einen Sattelpunkt an den Stellen
![]() für gerades
für gerades
![]() .
.
Ist
![]() ungerade, so ist
ungerade, so ist
![]() , und folglich
, und folglich
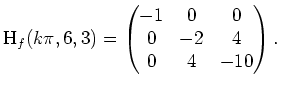
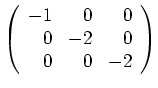 . Also ist sie negativ definit,
und somit besitzt
. Also ist sie negativ definit,
und somit besitzt