Es wird
und
Die notwendige Bedingung für lokale Extrema
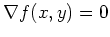 liefert die zu erfüllenden Gleichungen
liefert die zu erfüllenden Gleichungen
Aus der ersten Gleichung erhalten wir
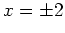 , und folglich aus der zweiten
, und folglich aus der zweiten
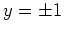 . Die kritischen Punkte sind somit gegeben durch
. Die kritischen Punkte sind somit gegeben durch
Es ist
negativ definit, und somit besitzt
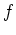 ein lokales Maximum in
ein lokales Maximum in
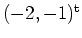 .
.
Es ist
indefinit, und folglich besitzt
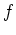 einen Sattelpunkt in
einen Sattelpunkt in
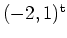 .
.
Es ist
positiv definit, und folglich besitzt
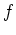 ein lokales Minimum in
ein lokales Minimum in
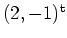 .
.
Es ist
indefinit, und folglich besitzt
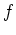 einen Sattelpunkt in
einen Sattelpunkt in
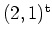 .
.
Skizze von
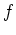 .
.
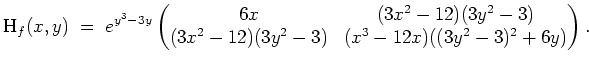
![]() liefert die zu erfüllenden Gleichungen
liefert die zu erfüllenden Gleichungen
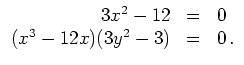
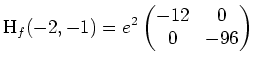
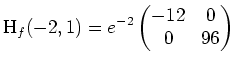
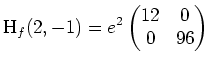
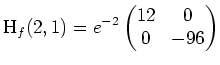
![]() .
.
![\includegraphics[width = 8cm]{l1.eps}](img17.png)