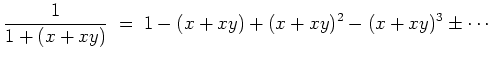Es ist
![]() in einer offenen Umgebung von
in einer offenen Umgebung von
![]() beliebig oft stetig differenzierbar.
beliebig oft stetig differenzierbar.
Zunächst werden
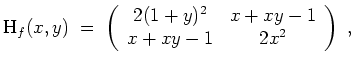
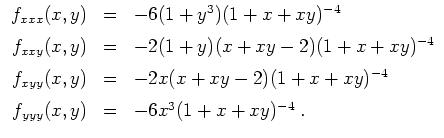
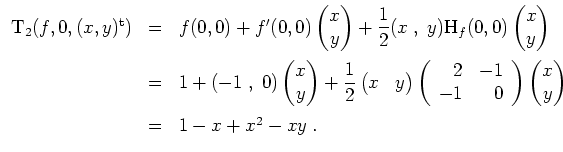
Für ein (später zu spezifizierendes)
![]() gibt es nach dem Satz von Taylor für jedes
gibt es nach dem Satz von Taylor für jedes
![]() ein
ein
![]() mit
mit
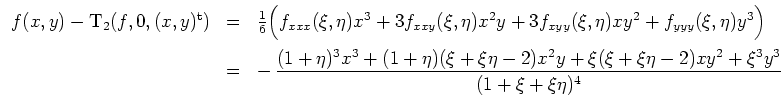
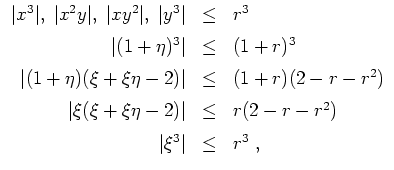
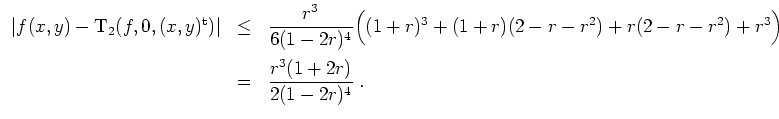
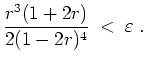
Sei nun zusätzlich
![]() angenommen. Dann genügt
angenommen. Dann genügt
![]() , d.h.
, d.h.
Fassen wir noch einmal zusammen. Für
![]() ist
ist