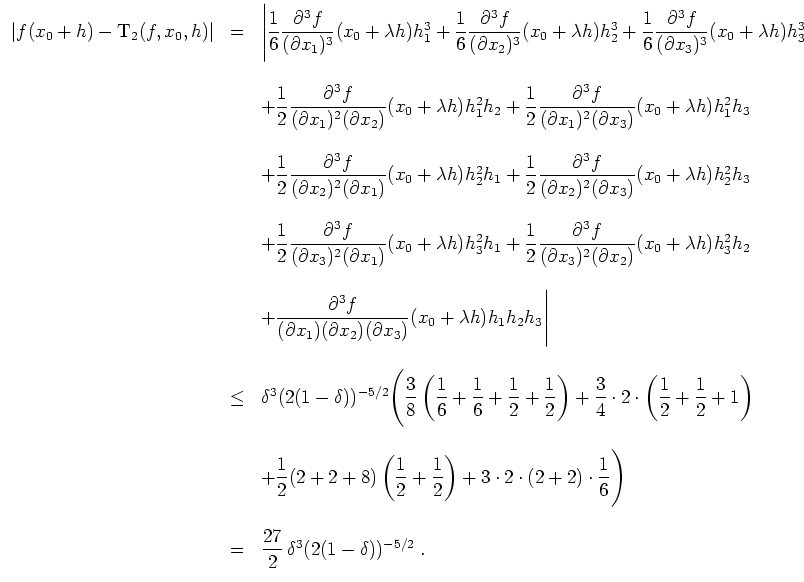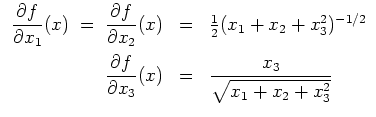
Sodann werden
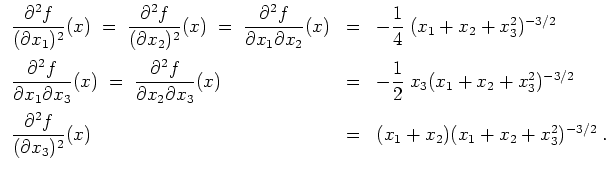
Also ergibt sich
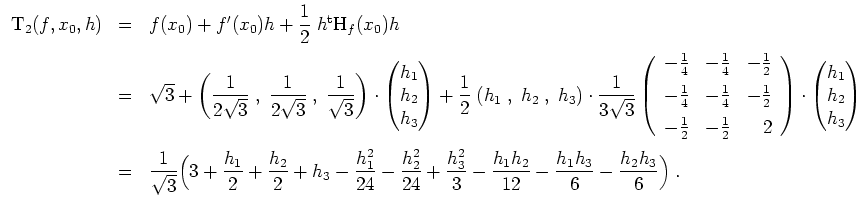
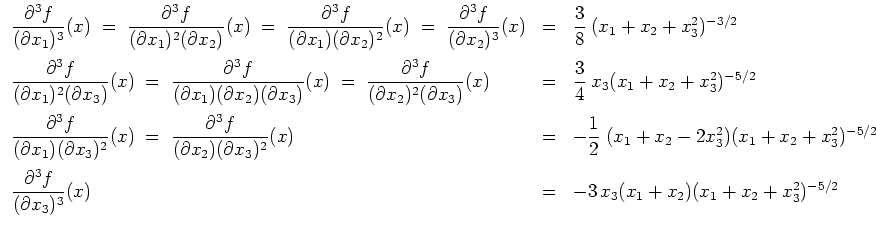
Beachte, daß
![]() für
für
![]() mit
mit
![]() .
.
Verwende ferner die Abschätzungen
![]() .
.
Für den Betrag des Restglieds liefert der Satz von Taylor mit einem
![]() für
für
![]() die Abschätzung
die Abschätzung
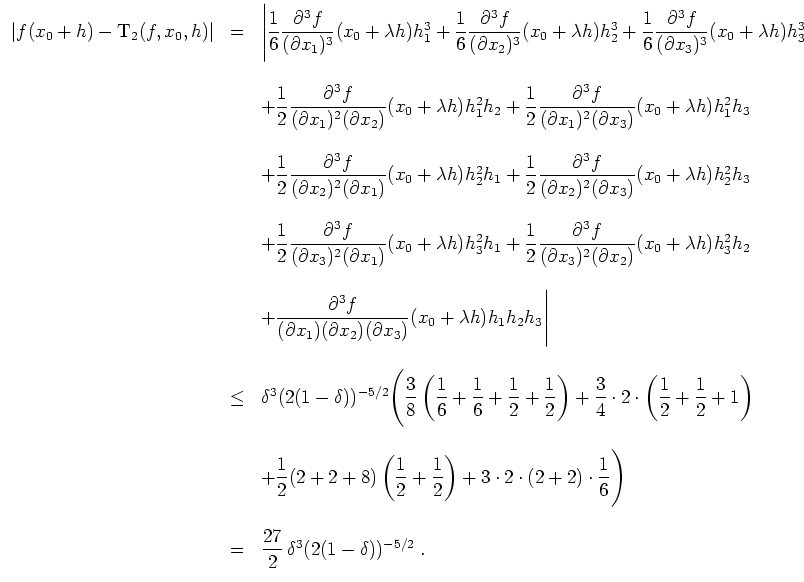
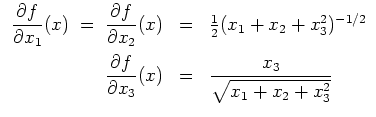
Sodann werden
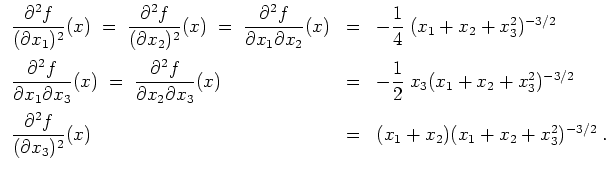
Also ergibt sich
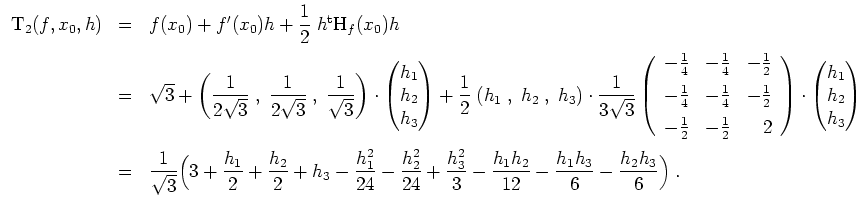
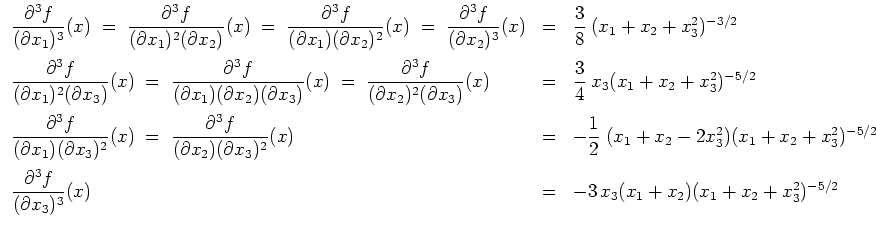
Beachte, daß
![]() für
für
![]() mit
mit
![]() .
.
Verwende ferner die Abschätzungen
![]() .
.
Für den Betrag des Restglieds liefert der Satz von Taylor mit einem
![]() für
für
![]() die Abschätzung
die Abschätzung